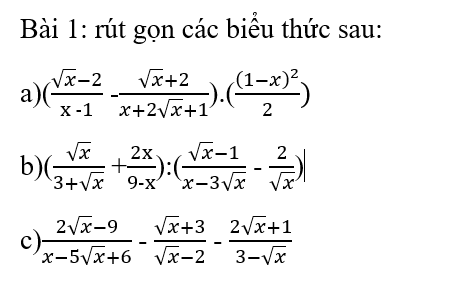Cho góc nhọn xOy, trên tia Ox lấy hai điểm A,A' ; trên tia Oy lấy hai điểm B, B' sao cho các điểm lấy không trùng với O. CMR: \(\dfrac{StOAB}{StOA'B'}=\dfrac{OA.OB}{OA'.OB'}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi thời gian làm một mình của tổ 1 là: `x` (giờ)
Thời gian làm một mình của tổ 2 là: `y` (giờ)
ĐK: `x,y>0`
Hai tổ cùng làm thì 15h xong nên ta có pt: `1/x+1/y=1/15` (1)
Nếu tổ 1 làm trong 3h và tổ 2 làm trong 5h thì được 25% công việc nên ta có pt:
\(\dfrac{3}{x}+\dfrac{5}{y}=\dfrac{1}{4}\left(2\right)\)
Từ (1) và (2) ta có hpt:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{15}\\\dfrac{3}{x}+\dfrac{5}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{15}\\3\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+\dfrac{2}{y}=\dfrac{1}{4}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{15}\\\dfrac{1}{5}+\dfrac{2}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{15}\\\dfrac{2}{y}=\dfrac{1}{4}-\dfrac{1}{5}=\dfrac{1}{20}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{40}=\dfrac{1}{15}\\y=2:\dfrac{1}{20}=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{15}-\dfrac{1}{40}=\dfrac{1}{24}\\y=40\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=24\\y=40\end{matrix}\right.\left(tm\right)\)
Vậy: ...

\(2x^2-5x-7\\ =\left(2x^2+2x\right)+\left(-7x-7\right)\\ =2x\left(x+1\right)-7\left(x+1\right)\\ =\left(2x-7\right)\left(x+1\right)\)

\(A=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{a-\sqrt{a}}\right):\dfrac{\sqrt{a}+1}{a-1}\left(a>0;a\ne1\right)\\ =\left[\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right]:\dfrac{\sqrt{a}+1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\\ =\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}-1}\right):\dfrac{1}{\sqrt{a}-1}\\ =\dfrac{\sqrt{a}-1}{\sqrt{a}-1}:\dfrac{1}{\sqrt{a}-1}\\ =1:\dfrac{1}{\sqrt{a}-1}\\ =\sqrt{a}-1\)

gọi x là quãng đường ab (km) (a>40)
vận tốc ô tô là \(40\times1.25\) = 50 (km/giờ)
thời gian xe máy đi được khi xe ô tô khởi hành đến khi gặp xe ô tô là \(\dfrac{x}{2\times40}\)=\(\dfrac{x}{80}\) (giờ)
thời gian xe ô tô đi được đến khi gặp xe máy là \(\dfrac{x}{2\times50}\) =\(\dfrac{x}{100}\)(giờ)
do ô tô gặp xe máy ở chính giữa đoạn đường
\(\Rightarrow\) \(\dfrac{x}{80}\) \(-\dfrac{x}{100}\)= 1
\(\Leftrightarrow\dfrac{5x}{400}-\dfrac{4x}{400}=1\)
\(\Leftrightarrow5x-4x=400\)
\(\Leftrightarrow x=400\) (thỏa mãn)
vậy quãng đường ab dìa 400 km
Gọi độ dài quãng đường AB là: `x` (km)
ĐK: x>0
Vận tốc của ô tô là: \(1,25\cdot40=50\left(km/h\right)\)
Do hai xe gặp nhau ở chính giữa đoạn đường nên ta có:
Thời gian xe máy đi thêm là: \(\left(\dfrac{1}{2}x-40\right):40=\dfrac{x}{80}-1\left(h\right)\)
Thời gian ô tô đi là: \(\dfrac{1}{2}x:50=\dfrac{x}{100}\) (h)
Do hai khoảng thời gian này bằng nhau nên ta có pt:
\(\dfrac{x}{100}=\dfrac{x}{80}-1\\ =>\dfrac{x}{80}-\dfrac{x}{100}=1\\ =>\dfrac{x}{400}=1\\ =>x=400\left(tm\right)\)
Vậy: ...

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)
\(\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(1-x\right)^2}{2}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right)\cdot\dfrac{\left(\sqrt[]{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)^2}{2}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\cdot\dfrac{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}-2}{1}\cdot\dfrac{\sqrt{x}-1}{2}=-\sqrt{x}\left(\sqrt{x}-1\right)\)
b: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne9\end{matrix}\right.\)
\(\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{2}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)-2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}-1-2\sqrt{x}+6}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt[]{x}-3\right)}{-\sqrt{x}+5}\)
\(=\dfrac{x+3\sqrt{x}}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}}{\sqrt{x}-5}=\dfrac{x}{\sqrt{x}-5}\)
c: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
\(\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

Số tiền mua bút bi và bút chì là \(279000-45000\cdot3=144000\left(đồng\right)\)
Tổng số bút bi và bút chì màu là 36 chiếc nên x+y=36
Số tiền mua bút bi là 3600x(đồng)
Số tiền mua bút chì màu là 5000y(đồng)
Tổng số tiền là 144000 đồng nên 3600x+5000y=144000
=>36x+50y=144
=>18x+25y=72
Do đó, hệ hai phương trình là: \(\left\{{}\begin{matrix}x+y=36\\18x+25y=72\end{matrix}\right.\)

A B C a b c H K
a/ Dựng \(AH\perp BC\left(H\in BC\right)\)
Xét tg vuông ACH có
\(\cos C=\dfrac{CH}{AC}=\dfrac{CH}{b}\Rightarrow CH=b\cos C\)
Xét tg vuông ABH có
\(\cos B=\dfrac{BH}{AB}=\dfrac{BH}{c}\Rightarrow BH=c\cos B\)
\(\Rightarrow CH+BH=BC=a=b\cos C+c\cos B\)
b/
Đặt \(\widehat{BAH}=\alpha;\widehat{CAH}=\beta\)
\(\Rightarrow\cos A=\cos\left(\alpha+\beta\right)=\cos\alpha\cos\beta-\sin\alpha\sin\beta=\)
\(=\dfrac{AH}{c}.\dfrac{AH}{b}-\dfrac{BH}{c}.\dfrac{CH}{b}=\dfrac{AH^2-BH.CH}{bc}=\)
\(=\dfrac{2AH^2-2BH.CH}{2bc}=\dfrac{c^2-BH^2+b^2-CH^2-2BH.CH}{2bc}=\)
\(=\dfrac{b^2+c^2-\left(BH+CH\right)^2}{2bc}=\dfrac{b^2+c^2-a^2}{2bc}\)

\(x^4+2x^2-3\\ =\left(x^4-x^2\right)+\left(3x^2-3\right)\\ =x^2\left(x^2-1\right)+3\left(x^2-1\right)\\ =\left(x^2-1\right)\left(x^2+3\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2+3\right)\)
\(x^4+2x^2-3\)
\(=x^4+3x^2-x^2-3\)
\(=x^2\left(x^2+3\right)-\left(x^2+3\right)=\left(x^2+3\right)\left(x^2-1\right)\)
\(=\left(x^2+3\right)\left(x-1\right)\left(x+1\right)\)

Đặt: \(3x^2-5x-7=0\)
\(\Delta=\left(-5\right)^2-4\cdot3\cdot\left(-7\right)=109>0\)
\(x_1=\dfrac{-\left(-5\right)+\sqrt{109}}{2\cdot3}=\dfrac{5+\sqrt{109}}{6}\)
\(x_2=\dfrac{-\left(-5\right)-\sqrt{109}}{2\cdot3}=\dfrac{5-\sqrt{109}}{6}\)
=> \(3x^2-5x-7=\left(x-\dfrac{5+\sqrt{109}}{6}\right)\left(x-\dfrac{5-\sqrt{109}}{6}\right)\)