x³(x+2)-2(x³-2³)-2x(x²-2²)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a;
A(\(x\)) = \(x^3\) - 4\(x\) + a - 3; B(\(x\)) = \(x-2\)
Theo bezout ta có:
A(\(x\)) ⋮ B(\(x\)) ⇔ A(2) = 0
Thay \(x\) = 2 vào biểu thức A(\(x\)) = \(x^3\) - 4\(x\) + a - 3 = 0 ta có:
A(2) = 23 - 4.2 + a - 3 = 0
8 - 8 + a - 3 = 0
a - 3 = 0
a = 3
Vậy a = 3 thì A(\(x\)) ⋮ B(\(x\))

a: \(5x^2\left(2x^3-4x^2+3x-1\right)\)
\(=5x^2\cdot2x^3-5x^2\cdot4x^2+5x^2\cdot3x-5x^2\cdot1\)
\(=10x^5-20x^4+15x^3-5x^2\)
b: \(\left(x^2-3x\right)\left(x^2-2x-8\right)\)
\(=x^4-2x^3-8x^2-3x^3+6x^2+24x\)
\(=x^4-5x^3-2x^2+24x\)
c: \(1225x^7:\left(-25x^2\right)\)
\(=\left(-1225:25\right)\cdot\left(x^7:x^2\right)\)
\(=-49x^5\)
d: \(\left(-10x^3+25x^2-8x\right):\left(-5x\right)\)
\(=\dfrac{10x^3}{5x}-\dfrac{25x^2}{5x}+\dfrac{8x}{5x}\)
\(=2x^2-5x+\dfrac{8}{5}\)
e: \(\left(3x^4-8x^3+11x^2+8x-5\right):\left(3x^2-2x+3\right)\)
\(=\dfrac{3x^4-2x^3+3x^2-6x^3+4x^2-6x+4x^2-\dfrac{8}{3}x+4+\dfrac{50}{3}x-9}{3x^2-2x+3}\)
\(=x^2-2x+\dfrac{4}{3}+\dfrac{\dfrac{50}{3}x-9}{3x^2-2x+3}\)

\(-2x^4+3x^5+x^3+4x+14x^4-6x^5-x^3+x+10\)
\(=\left(3x^5-6x^5\right)+\left(-2x^4+14x^4\right)+\left(x^3-x^3\right)+\left(4x+x\right)+10\)
\(=-3x^5+12x^4+5x+10\)
`#NqHahh`
-2x⁴ + 3x⁵ + x³ + 4x + 14x⁴ - 6x⁵ - x³ + x + 10
= (3x⁵ - 6x⁵) + (-2x⁴ + 14x⁴) + (x³ - x³) + (4x + x) + 10
= -3x⁵ + 12x⁴ + 5x + 10

Chứng minh tam giác là tam giác cân, ta có thể chứng minh:
- Tam giác có hai cạnh bằng nhau.
- Tam giác có hai góc bằng nhau.
- Tam giác có hai trong bốn đường: đường trung tuyến, đường trung trực, đường cao, đường phân giác cùng xuất phát từ một đỉnh.

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
=>BA=BD
mà BA>BH(ΔBAH vuông tại H)
nên BH<BD
=>H thuộc đoạn BD
b: Ta có: ΔBAE=ΔBDE
=>EA=ED
=>E nằm trên đường trung trực của AD(1)
Ta có: BA=BD
=>B nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra BE là đường trung trực của AD
c: Xét ΔBAD có
BE,AH là các đường cao
BE cắt AH tại O
Do đó: O là trực tâm của ΔBAD
=>DO\(\perp\)AB
mà AC\(\perp\)AB
nên DO//AC
d: Ta có: \(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔHDA vuông tại H)
mà \(\widehat{BAD}=\widehat{BDA}\)(BA=BD)
nên \(\widehat{CAD}=\widehat{HAD}\)
=>AD là phân giác của góc HAC
Xét ΔAHC có AD là phân giác
nên \(\dfrac{DH}{DC}=\dfrac{AH}{AC}\)
mà AH<AC
nên DH<DC

Có: \(A\left(x\right)=x^4+2x^2-x\) và \(B\left(x\right)=-x^4-\dfrac{1}{2}x^2+2x-8\)
+, \(C\left(x\right)=A\left(x\right)+B\left(x\right)\)
\(=\left(x^4+2x^2-x\right)+\left(-x^4-\dfrac{1}{2}x^2+2x-8\right)\)
\(=x^4+2x^2-x-x^4-\dfrac{1}{2}x^2+2x-8\)
\(=\dfrac{3}{2}x^2+x-8\)
+, \(D\left(x\right)=B\left(x\right)-A\left(x\right)\)
\(=\left(-x^4-\dfrac{1}{2}x^2+2x-8\right)-\left(x^4+2x^2-x\right)\)
\(=-x^4-\dfrac{1}{2}x^2+2x-8-x^4-2x^2+x\)
\(=-2x^4-\dfrac{5}{2}x^2+3x-8\)
b) Ta có: \(C\left(x\right)=\dfrac{3}{2}x^2+x-8\)
\(\Rightarrow C\left(2\right)=\dfrac{3}{2}\cdot2^2+2-8=0\)
\(\Rightarrow x=2\) là 1 nghiệm của \(C\left(x\right)\)
c) Có: \(E\left(x\right)+D\left(x\right)=2x^4\)
\(\Rightarrow E\left(x\right)=2x^4-D\left(x\right)\)
\(=2x^4-\left(-2x^4-\dfrac{5}{2}x^2+3x-8\right)\)
\(=2x^4+2x^4+\dfrac{5}{2}x^2-3x+8\)
\(=4x^4+\dfrac{5}{2}x^2-3x+8\)

a: Ta có: DE\(\perp\)AC
AB\(\perp\)AC
Do đó: DE//AB
=>\(\widehat{CHE}=\widehat{CBA}=65^0\)
b: Sửa đề: ΔBAD cân
Xét ΔBIA vuông tại I và ΔBID vuông tại I có
BI chung
IA=ID
Do đó; ΔBIA=ΔBID
=>BA=BD
=>ΔBAD cân tại B
c: Xét ΔCAD có
CI,DE là các đường cao
CI cắt DE tại H
Do đó: H là trực tâm của ΔCAD
=>AH\(\perp\)CD


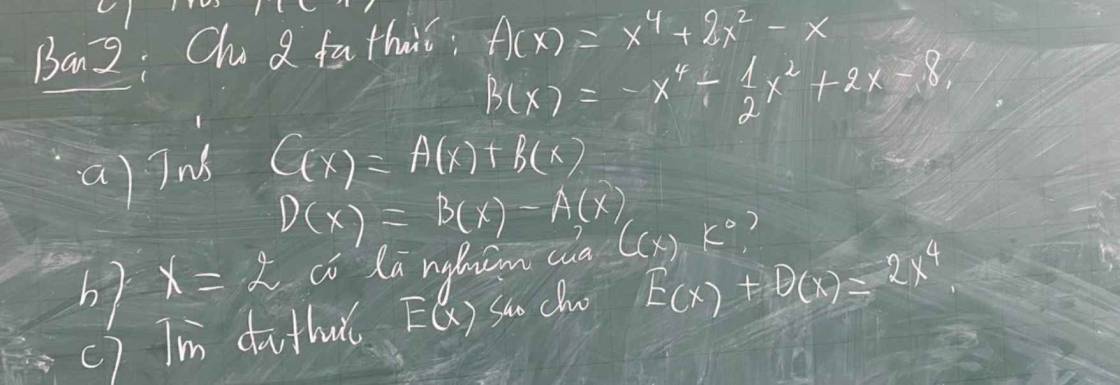
Em cần làm gì với biểu thức này.