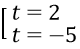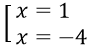Tìm m để phương trình \(\frac{mx+2}{\sqrt{x-2}}=\sqrt{x-2}\) vô nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TP
0
NM
1
DD
Đoàn Đức Hà
Giáo viên
30 tháng 11 2020
\(\hept{\begin{cases}\sqrt{12-2x^2}=4+y\\\sqrt{1-2y-y^2}=5-2x\end{cases}}\)(ĐK: \(\hept{\begin{cases}12-2x^2\ge0\\1-2y-y^2\ge0\end{cases}}\))
\(\Rightarrow\hept{\begin{cases}12-2x^2=\left(4+y\right)^2\\1-2y-y^2=\left(5-2x\right)^2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y^2+2x^2+8y+4=0\\4x^2+y^2-20x+2y+24=0\end{cases}}\)
\(\Rightarrow2\left(4x^2+y^2-20x+2y+24\right)+\left(y^2+2x^2+8y+4\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x-y-4\right)^2+8\left(x-2\right)^2+\left(y+2\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\y=-2\end{cases}}\)
Thử lại thỏa mãn.
XO
30 tháng 11 2020
Ta có |x + 3| + |7 - x| \(\ge\left|x+3+7-x\right|=\left|10\right|=10\)
Dấu "=" xảy ra <=> \(\left(x+3\right)\left(7-x\right)\ge0\)
Xét các trường hợp
TH1 : \(\hept{\begin{cases}x+3\ge0\\7-x\ge0\end{cases}}\Rightarrow\hept{\begin{cases}x\ge-3\\x\le7\end{cases}}\Rightarrow-3\le x\le7\)(tm)
TH2 \(\hept{\begin{cases}x+3\le0\\7-x\le0\end{cases}}\Rightarrow\hept{\begin{cases}x\le-3\\x\ge7\end{cases}}\left(\text{loại}\right)\)
Vậy \(-3\le x\le7\)là giá trị cần tìm
KQ
0
KQ
1
DD
Đoàn Đức Hà
Giáo viên
30 tháng 11 2020
\(\sqrt{x}+\sqrt{9-x}=\sqrt{-x^2+9x+9}\)(ĐK: \(0\le x\le9\))
\(\Leftrightarrow x+9-x+2\sqrt{x\left(9-x\right)}=-x^2+9x+9\)
\(\Leftrightarrow4x\left(9-x\right)=x^2\left(9-x\right)^2\)
\(\Leftrightarrow\orbr{\begin{cases}x\left(9-x\right)=0\\x\left(9-x\right)=4\end{cases}}\)
- \(x\left(9-x\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=9\end{cases}}\).
- \(x\left(9-x\right)=4\Leftrightarrow\orbr{\begin{cases}x=\frac{9+\sqrt{65}}{2}\\x=\frac{9-\sqrt{65}}{2}\end{cases}}\)
KQ
1
TH
29 tháng 11 2020
ĐKXĐ: \(X\ge1\)
<=> \(\left(\sqrt{x+1}-\sqrt{x-1}=1\right)^2=1\) ( dựa vào điều kiện trên)
<=> \(X+1-2\sqrt{X^2-1}+X-1=1\)
<=>\(\left(2\sqrt{X^2-1}\right)^2=\left(2X-1\right)^2\)
<=>\(4X^2-4=4X^2-4X+1\)
<=> X= \(\frac{-5}{4}\)( K/TM)
Vậy phương trình vô nghiệm
TH
29 tháng 11 2020
(x+5)(2-x)=3\(\sqrt{x^2+3x}\)
<=> -x2-3x+10= 3\(\sqrt{x^2+3x}\)
⇔ x2 + 3x + 3√(x2 + 3x) - 10 = 0
Đặt t = √(x2 + 3x), t ≥ 0. Phương trình đã cho trở thành
t2 + 3t - 10 = 0 ⇔ 
Vì t ≥ 0 ⇒ t = 2, thay vào ta có √(x2 + 3x) = 2
⇔ x2 + 3x - 4 = 0 ⇔ 
Vậy phương trình có nghiệm là x = 1 và x = -4