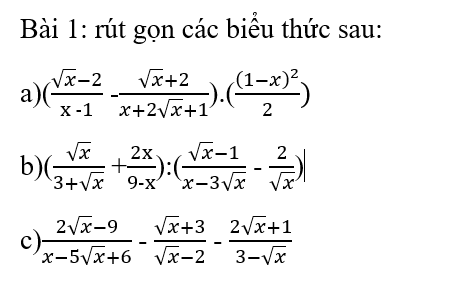\(\left(x+y\right)^2+\left(x-y\right)^2+\left(x+y\right)\left(x-y\right)\\ =\left(x^2+2xy+y^2\right)+\left(x^2-2xy+y^2\right)+\left(x^2-y^2\right)\\ =x^2+2xy+y^2+x^2-2xy+y^2+x^2-y^2\\ =3x^2+y^2\)

Ta có: \(\left\{{}\begin{matrix}3x^2\ge0\forall x\\y^2\ge0\forall y\end{matrix}\right.=>3x^2+y^2\ge0\forall x,y\)

=> Biểu thức không âm với mọi x và y 

`(x+y)^2 + (x - y)^2 + (x+y)(x - y)`

`= x^2 + 2xy + y^2 + x^2 - 2xy + y^2 + x^2 - y^2`

`= 3x^2 + y^2`

Ta có: \(\left\{{}\begin{matrix}x^2\ge0\\y^2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2\ge0\\y^2\ge0\end{matrix}\right.\)

`=> 3x^2 + y^2 ≥ 0`

Vậy đa thức trên luôn không âm với mọi `x;y`

ta có 2n+12= 2(n + 6)

suy ra để 2n+12 chia hết cho n+3 thì 

2(n + 6) chia hết cho n+3

nên n + 6 chia hết n +3

rồi làm tiếp nhé :)

Ta có \(n+3⋮n+3\) với mọi số tự nhiên \(n\)

nên \(2\left(n+3\right)=2n+6⋮n+3\)

Mà \(2n+12=2n+6+6\)

Do đó để \(2n+12⋮n+3\) thì \(6⋮n+3\)

nên \(n+3\) thuộc \(U'\left(6\right)=\text{1; 2; 3; 6}\)

Giải từng trường hợp ta được: \(n=0;3\)

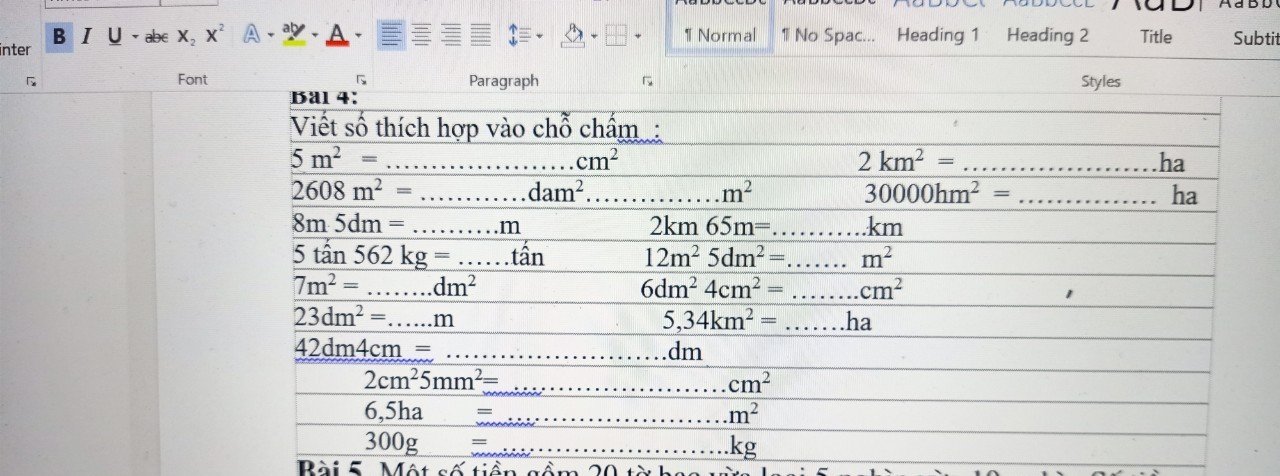
Bài 3: 

a: \(6,5m=6m5dm\)

2,10m=2m10cm

8,09kg=8kg90g

9,6 tấn=9 tấn 600kg

b: 4,7m²=47000cm²

\(43567mm^2=435cm^267mm^2\)

\(6,08cm^2=6cm^28mm^2\)

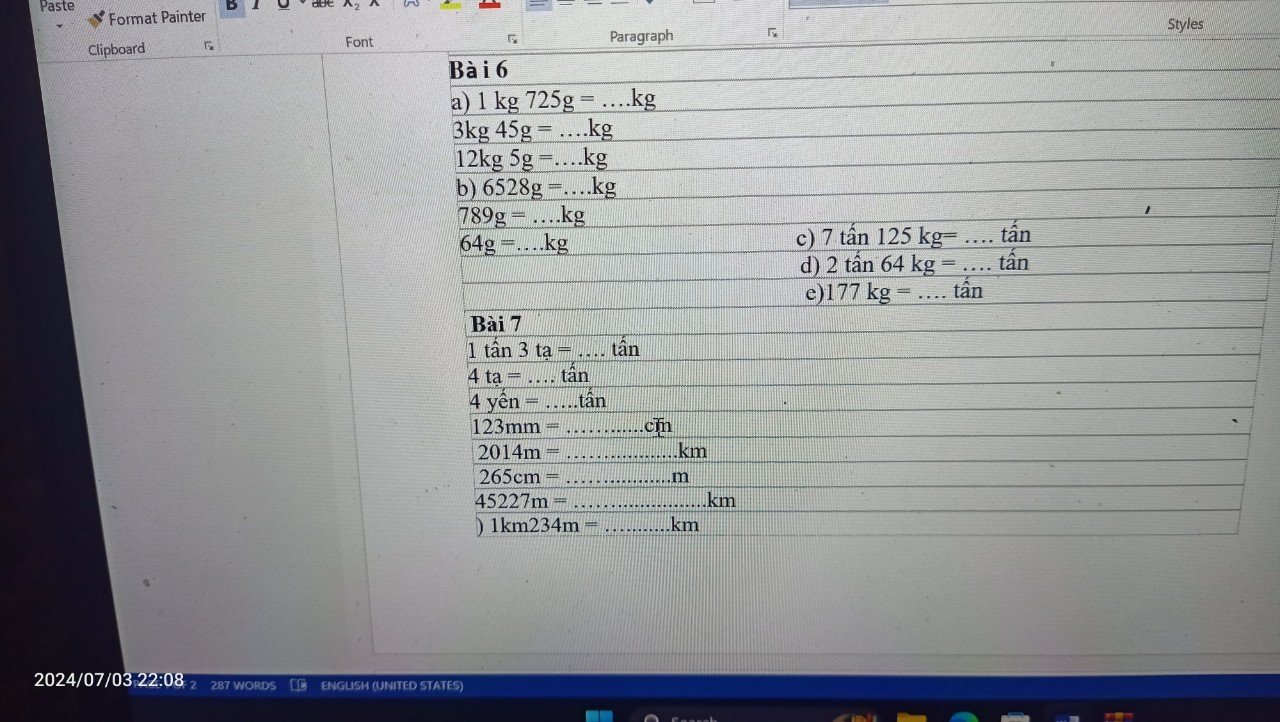
Bài 2:

a: \(1kg324g=1,324kg\)

30kg27g=30,027kg

12dg5g=12,05dg

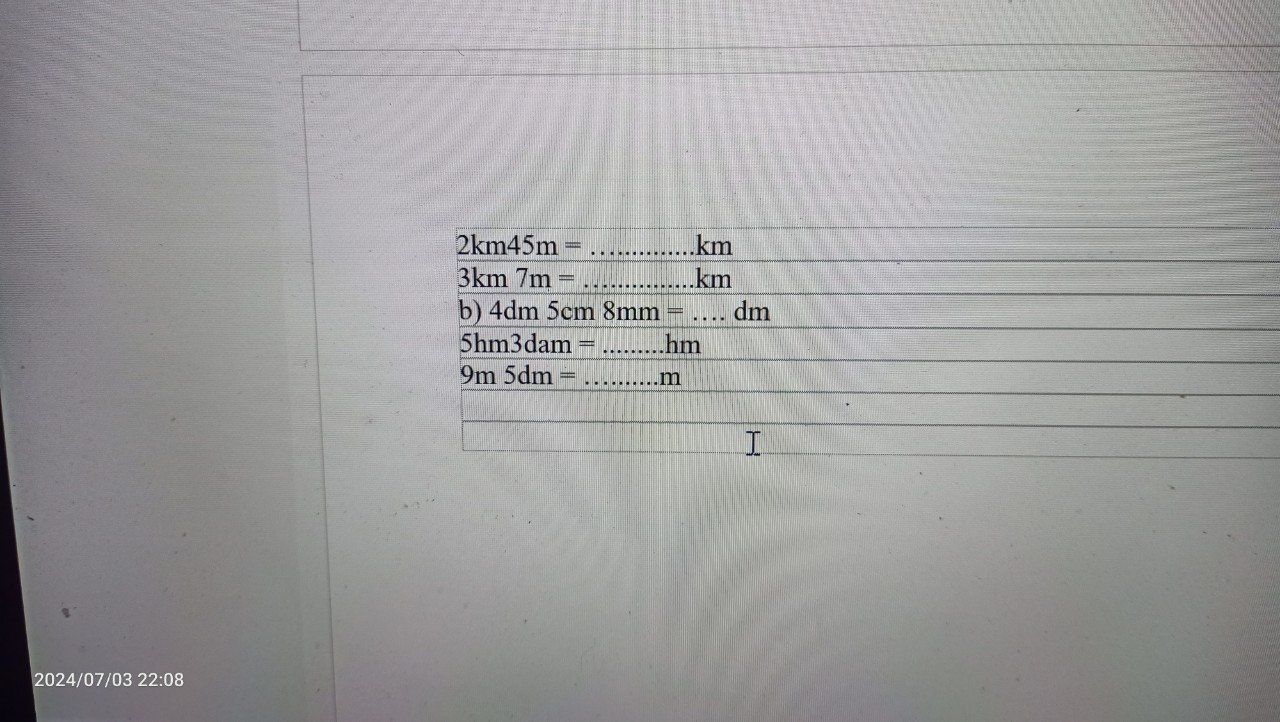
b: \(9km528m=9,528km\)

7hm89m=78,9dam

\(6m48cm=6,48m\)

c: \(7m^225dm^2=7,25m^2\)

\(2dm^264cm^2=2,64dm^2\)

\(1cm^2234mm^2=3,34cm^2\)

a/

Xét tg vuông AME và tg vuông AHC có

AE=AC (gt)

\(\widehat{EAM}+\widehat{HAC}=\widehat{ACH}+\widehat{HAC}=90^o\Rightarrow\widehat{EAM}=\widehat{ACH}\)

=> tg AME = tg AHC (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)

=> AM=AH

C/m tương tự khi xét tg vuông AKD và tg vuông AHB

=> DK=AH

=> DK=EM

b/

\(DK\perp AH\left(gt\right);EM\perp AH\left(gt\right)\) => DK//EM (cùng vg với AH)

DK=EM (cmt)

=> EKDM là hình bình hành (Tứ giác có cặp cạnh đối // và bằng nhau là hbh)

=> IE=ID (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)

Số bưu ảnh của Hoa là:

(134+14-16):3=132:3=44(cái)

Số bưu ảnh của hồng là 44-14=30(cái)

Số bưu ảnh của Huệ là 44+16=60(cái)

\(3^{400}=\left(3^4\right)^{100}=81^{100};5^{300}=\left(5^3\right)^{100}=125^{100}\)

mà 81<125

nên \(3^{400}< 5^{300}\)

Ta có : 

3^400 = (3^4)^100 = 81^100

5^300 = (5^3)^100 = 125^100

Vì 81^100 < 125^100 nên

=>3^400 < 5^300

Vậy 3^400 < 5^300

Số tự nhiên chia 2 dư 1 có dạng tổng quát là \(2k+1\)

Bài 2: 

a: Xét ΔABC vuông tại A có

\(sin\alpha=sinB=\dfrac{AC}{BC}\)

\(cos\alpha=cosB=\dfrac{AB}{BC}\)

\(tan\alpha=tanB=\dfrac{AC}{AB}\)

\(cot\alpha=cotB=\dfrac{AB}{AC}\)

b: \(sin^2\alpha+cos^2\alpha=\left(\dfrac{AB}{BC}\right)^2+\left(\dfrac{AC}{BC}\right)^2\)

\(=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\)

\(tan\alpha=\dfrac{AC}{AB}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{sin\alpha}{cos\alpha}\)

\(cot\alpha=\dfrac{AC}{AB}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{cos\alpha}{sin\alpha}\)

c: 

A: \(sin^2\alpha+cos^2\alpha=sin^2\left(\dfrac{1}{3}\right)+cos^2\left(\dfrac{1}{3}\right)=1\)

B: \(\dfrac{sin35^0}{cos35^0}\cdot tan55^0+\dfrac{cos55^0}{sin55^0}\cdot cot55^0\)

\(=\dfrac{cos55}{sin55}\cdot\dfrac{sin55^0}{cos55^0}+\dfrac{cos55^0}{sin55^0}\cdot tan55^0\)

=1+1

=2

C: \(cos^242^0+cos^253^0+cos^248^0+cos^237^0+cos^245^0\)

\(=\left(sin^242^0+cos^242^0\right)+\left(sin^237^0+cos^237^0\right)+\dfrac{1}{2}\)

\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)

\(\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(1-x\right)^2}{2}\)

\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right)\cdot\dfrac{\left(\sqrt[]{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)^2}{2}\)

\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\cdot\dfrac{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)^2}{2}\)

\(=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}-2}{1}\cdot\dfrac{\sqrt{x}-1}{2}=-\sqrt{x}\left(\sqrt{x}-1\right)\)

b: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne9\end{matrix}\right.\)

\(\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\)

\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{2}{\sqrt{x}}\right)\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)-2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}-1-2\sqrt{x}+6}{\sqrt{x}\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt[]{x}-3\right)}{-\sqrt{x}+5}\)

\(=\dfrac{x+3\sqrt{x}}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}}{\sqrt{x}-5}=\dfrac{x}{\sqrt{x}-5}\)

c: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)

\(\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)

\(=\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\)

\(=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)