Tìm các cặp số nguyên(x,y) thỏa mãn x^2y - 5y - 8x - 1 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để chứng minh rằng (2 + \frac{3}{2} + \frac{5}{2}) là số vô tỉ, ta cần chứng minh rằng tổng này không thể biểu diễn dưới dạng một tỉ số của hai số nguyên. Để làm điều này, ta có thể chứng minh bằng phản chứng, giả sử rằng tổng đó là một số tỉ.
nhớ tick cho mik nhé

Gọi chiều rộng hình chữ nhật là x(cm)
(Điều kiện: x>0)
Chiều dài hình chữ nhật là 3x(cm)
Chiều dài sau khi giảm đi 5cm là 3x-5(cm)
Chiều rộng sau khi tăng thêm 5cm là x+5(cm)
Diện tích tăng thêm 155cm2 nên ta có:
(3x-5)(x+5)-3x*x=155
=>\(3x^2+15x-5x-25-3x^2=155\)
=>10x=155+25=180
=>x=18(nhận)
Chiều dài hình chữ nhật là \(3\cdot18=54\left(cm\right)\)
Diện tích hình chữ nhật là \(18\cdot54=972\left(cm^2\right)\)

1,53x72+15,3x5,2-1,53x24
=1,53x72+1,53x52-1,53x24
=1,53x(72+52-24)
=1,53x100=153

\(F=-1-\dfrac{1}{3}-\dfrac{1}{6}-...-\dfrac{1}{1225}\)
\(=-2\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{2450}\right)\)
\(=-2\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)\)
\(=-2\left(1-\dfrac{1}{50}\right)=-2\cdot\dfrac{49}{50}=-\dfrac{49}{25}\)

Đây là toán nâng cao chuyên đề chu vi diện tích hình ghép, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Tổng chiều dài lúc sau và chiều rộng lúc đầu là:
153 : 3 = 51 (m)
Tổng của chiều dài lúc đầu và chiều rộng lúc đầu là:
51 - 3 = 48 (m)
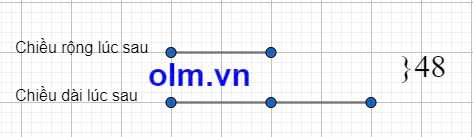
Ta có sơ đồ:
Theo sơ đồ ta có:
Chiều dài lúc đầu là:
48: (1 + 2) x 2 = 32 (m)
Chiều rộng lúc đầu là:
48 - 32 = 16 (m)
Diện tích lúc đầu của hình chữ nhật là:
32 x 16 = 512 (m2)
Đáp số: 512 m2

\(\dfrac{2}{4}\times\dfrac{5}{10}\times\dfrac{7}{11}=\dfrac{7}{11}\times\dfrac{1}{2}\times\dfrac{1}{2}=\dfrac{7}{44}\)
\(\dfrac{2}{4}\) x \(\dfrac{5}{10}\) x \(\dfrac{7}{11}\)
= \(\dfrac{1}{4}\) x \(\dfrac{7}{11}\)
= \(\dfrac{7}{44}\)

Để giải hệ phương trình này, chúng ta có thể sử dụng phương pháp giải hệ phương trình bằng cách loại bỏ biến một cách tuần tự. Dưới đây là cách giải:
-
Từ phương trình thứ nhất: (xy + 2y = 4x + 6) Ta có thể viết lại thành: (2y + xy = 4x + 6) (y(2 + x) = 4x + 6) (y = \frac{4x + 6}{2 + x})
-
Từ phương trình thứ hai: (yz + 4z = 6y) Ta có thể viết lại thành: (4z + yz = 6y) (z(4 + y) = 6y) (z = \frac{6y}{4 + y})
-
Từ phương trình thứ ba: (zx + 6x = 2z) Ta có thể viết lại thành: (6x + zx = 2z) (x(6 + z) = 2z) (x = \frac{2z}{6 + z})
-
Substitute (y) từ phương trình thứ nhất vào phương trình thứ ba, ta được: (y = \frac{4(\frac{2z}{6 + z}) + 6}{2 + \frac{2z}{6 + z}})
-
Substitute (z) từ phương trình thứ hai vào phương trình thứ ba, ta được: (x = \frac{2(\frac{6(\frac{6y}{4 + y})}{4 + (\frac{6y}{4 + y})})}{6 + \frac{6y}{4 + y}})
Từ đó, chúng ta có thể tìm ra giá trị cụ thể của (x), (y), (z).

\(x^2y-5y-8x-1=0\)
\(\Leftrightarrow y\left(x^2-5\right)=8x+1\)
\(\Rightarrow y=\dfrac{8x+1}{x^2-5}\) (1)
y nguyên \(\Rightarrow\dfrac{8x+1}{x^2-5}\) nguyên
\(\Rightarrow8x+1⋮x^2-5\)
\(\Rightarrow x\left(8x+1\right)⋮x^2-5\)
\(\Rightarrow8\left(x^2-5\right)+x+40⋮x^2-5\)
\(\Rightarrow x+40⋮x^2-5\)
\(\Rightarrow8\left(x+40\right)-\left(8x+1\right)⋮x^2-5\)
\(\Rightarrow329⋮x^2-5\)
\(\Rightarrow x^2-5\inƯ\left(329\right)\)
Mà \(x^2-5\ge-5;\forall x\)
\(\Rightarrow x^2-5\in\left\{-1;1;11;29;319\right\}\)
\(\Rightarrow x^2\in\left\{4;6;16;34;324\right\}\)
\(\Rightarrow x^2\in\left\{4;16;324\right\}\) do \(x^2\) là SCP
\(\Rightarrow x\in\left\{-18;-4;-2;2;4;18\right\}\)
Thay lần lượt vào (1) ta được: \(\left(x;y\right)=\left(-2;15\right);\left(2;-17\right);\left(4;3\right)\)