
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Áp dụng định lý Viet:
$x_1+x_2=\frac{7}{2}$
$x_1x_2=\frac{-3}{2}$
Khi đó:
$B=x_1^2x_2+x_2^2x_1-3x_1x_2=x_1x_2(x_1+x_2)-3x_1x_2$
$=\frac{-3}{2}.\frac{7}{2}-3.\frac{-3}{2}=\frac{-3}{4}$
2.
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m+1)^2-3(2m-1)\geq 0$
$\Leftrightarrow m^2-4m+4\geq 0$
$\Leftrightarrow (m-2)^2\geq 0\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=\frac{2(m+1)}{3}$
$x_1x_2=\frac{2m-1}{3}$
Để PT có 2 nghiệm $x_1,x_2<2$ thì:
\(\left\{\begin{matrix}
x_1+x_2< 4\\
(x_1-2)(x_2-2)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x_1+x_2<4\\
x_1x_2-2(x_1+x_2)+4>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{2(m+1)}{3}<4\\ \frac{2m-1}{3}-2.\frac{2(m+1)}{3}+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m<5\\ m< \frac{7}{2}\end{matrix}\right.\Leftrightarrow m< \frac{7}{2}\)
Vậy..........

a)9873
b)3789
Cảm ơn thầy ạ , thầy đã cho em cơ hội sửa sai ạ . ^^

Lời giải:
Gọi chiều dài và chiều rộng của khu đất lần lượt là $a$ và $b$ (m)
Theo bài ra ta có:
$ab=96$
$(a-1)(b+2)=ab+14$
$\Leftrightarrow ab+2a-b-2=ab+14$
$\Leftrightarrow 2a-b=16$
$\Leftrightarrow b=2a-16$. Thay vào điều kiện $ab=96$ suy ra:
$a(2a-16)=96$
$\Leftrightarrow a(a-8)=48$
$\Leftrightarrow a^2-8a-48=0$
$\Leftrightarrow (a+4)(a-12)=0$
Do $a>0$ nên $a=12$
$b=96:12=8$
Vậy chiều dài và chiều rộng khu đất lần lượt là $12$ m và $8$ m
Gọi chiều rộng và chiều dài khu đất lần lượt là a(m),b(m)
(Điều kiện: a>0; b>0)
Nếu tăng chiều rộng thêm 2m và giảm chiều dài đi 1m thì diện tích tăng thêm 14m2 nên ta có:
(a+2)(b-1)=ab+14
=>ab-a+2b-2=ab+14
=>-a+2b=16
=>a-2b=-16
=>a=2b-16
Diện tích là 96m2 nên ab=96
=>\(b\left(2b-16\right)=96\)
=>\(b\left(b-8\right)=48\)
=>\(b^2-8b-48=0\)
=>(b-12)(b+4)=0
=>\(\left[{}\begin{matrix}b=12\left(nhận\right)\\b=-4\left(loại\right)\end{matrix}\right.\)
Vậy: Chiều dài là 12m; Chiều rộng là 96:12=8(m)

\(A=2+2^2+2^3+...+2^{99}+2^{100}\)
Ta có: \(2A=2^2+2^3+2^4+...+2^{100}+2^{101}\)
\(2A-A=\left(2^2+2^3+2^4+...+2^{100}+2^{101}\right)-\left(2+2^2+2^3+...+2^{99}+2^{100}\right)\)
\(A=2^{101}-2\)
Vì \(2^{101}=2^{101}\)
\(\Rightarrow2^{101}-2< 2^{101}\)
Hay \(A< 2^{101}\)
Vậy \(A< 2^{101}\).
\(#NqHahh\)

Gọi tuổi của '' tôi '' trước đây là : a => tuổi của bạn là a/2
Tuổi bạn hiện này bằng a
Ta có :
a/2 + ( 27 - a ) = a
27 - a = a - a/2
27 - a = a/2
27 = a/2 + a
27 = a x 3/2
a = 27 : 3/2
a = 18
Vậy hiện nay bạn 18 tuổi
Like nhaa

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,M,O thẳng hàng

Giải:
Số dư là số dư lớn nhất có thể nên số dư là:
7 - 1 = 6
Số bị chia là:
19 x 7 + 6 = 139
Số bị chia là 139.
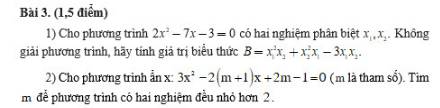


Lời giải:
a.
Vì $MC, MD$ là tiếp tuyến của $(O)$ nên $MC\perp OC, MD\perp OD$
$\Rightarrow \widehat{MCO}=\widehat{MDO}=90^0$
Tứ giác $MCOD$ có tổng 2 góc đối nhau $\widehat{MCO}+\widehat{MDO}=90^0+90^0=180^0$ nên $MCOD$ là tứ giác nội tiếp.
$\Rightarrow M,C,O,D$ cùng thuộc 1 đường tròn (1)
Mặt khác:
$K$ là trung điểm $AB$ nên $OK\perp AB$.
$\Rightarrow \widehat{MKO}=90^0$
Tứ giác $MCKO$ có $\widehat{MCO}=\widehat{MKO}=90^0$ và cùng nhìn cạnh $MO$ nên $MCKO$ là tứ giác nội tiếp.
$\Rightarrow M,C,K,O$ cùng thuộc 1 đường tròn (2)
Từ $(1); (2)\Rightarrow M,C,K,O,D$ cùng thuộc 1 đường tròn.
$\Rightarrow MCKD$ là tứ giác nội tiếp.
b.
Xét tam giác $MCA$ và $MBC$ có:
$\widehat{M}$ chung
$\widehat{MCA}=\widehat{MBC}$ (góc tạo bởi tt và dây cung bằng góc nt chắn cung đó)
$\Rightarrow \triangle MCA\sim \triangle MBC$ (g.g)
$\Rightarrow \frac{MC}{MA}=\frac{MB}{MC}\Rightarrow MC^2=MA.MB(3)$
Mặt khác:
Xét tam giác $MCN$ và $MKC$ có:
$\widehat{M}$ chung
$\widehat{MCN}=\widehat{MCD}=\frac{1}{2}\text{sđc(CD)}=\frac{1}{2}\widehat{COD}=\widehat{COM}=\widehat{MKC}$ (do $MCKO$ là tgnt)
$\Rightarrow \triangle MCN\sim \triangle MKC$ (g.g)
$\Rightarrow \frac{MC}{MK}=\frac{MN}{MC}$
$\Rightarrow MC^2=MK.MN(4)$
Từ $(3); (4)\Rightarrow MA.MB=MK.MN$
Hình vẽ: