Cho \(\widehat{AOB}\) vuông và tia OC nằm trong góc đó. Vẽ tia OX sao cho OA là tia phân giác của \(\widehat{xOC}\), vẽ tia Oy sao cho OB là tia phân giác của \(\widehat{yOC}\). Chứng tỏ Ox, Oy là hai tia đối nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


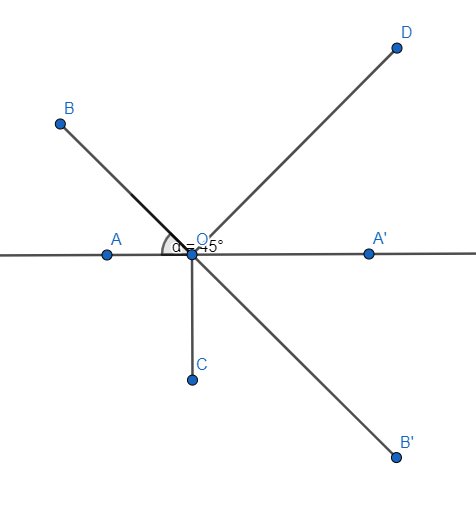
a) Vì OB' là tia phân giác của \(\widehat{A'OC}\) nên \(\widehat{A'OB'}=\dfrac{\widehat{A'OC}}{2}=\dfrac{90^o}{2}=45^o\). Suy ra \(\widehat{AOB}=\widehat{A'OB'}\left(=45^o\right)\). Lại có \(\widehat{AOB}+\widehat{BOA'}=\widehat{AOA'}=180^o\) nên \(\widehat{BOB'}=\widehat{A'OB'}+\widehat{BOA'}=180^o\) hay B, O, B' thẳng hàng. Suy ra \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là 2 góc đối đỉnh.
b) Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AA', ta thấy tia OB nằm giữa 2 tia OA và OD, tia OD lại nằm giữa 2 tia OB và OA', do đó \(\widehat{AOB}+\widehat{BOD}+\widehat{DOA'}=\widehat{AOA'}\) \(\Leftrightarrow45^o+90^o+\widehat{A'OD}=180^o\) \(\Leftrightarrow\widehat{A'OD}=45^o\)

a, |\(x\)| = \(\dfrac{1}{5}\)
\(\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=-\dfrac{1}{5}\end{matrix}\right.\)

a) 1 sào khoai lang năm 2021 thu hoạch được :
\(2:1,13=2,26\) (tấn)
b) Số tiền 1 sào khoai 2,26 tấn :
\(\left(2,26x9000000\right):2=10170000\) (đồng)
Số tiền bán được năm 2020 :
\(10170000:0,9=11300000\) (đồng)

a) \(\dfrac{32}{5}-\left(-\dfrac{9}{8}+\dfrac{12}{5}\right)+\left(\dfrac{-1}{2}\right)^3\)
\(=\dfrac{32}{5}+\dfrac{9}{8}-\dfrac{12}{5}-\dfrac{1}{8}\)
\(=\dfrac{32}{5}-\dfrac{12}{5}+\dfrac{9}{8}-\dfrac{1}{8}\)
\(=4+1\)
\(=5\)
b) \(\dfrac{15}{17}-3.\left(\dfrac{10}{3}+\dfrac{5}{17}\right)+\left(-1\right)^{2020}\)
\(=\dfrac{15}{17}-10-\dfrac{15}{17}+1=-9\)
c) \(6,5+1,2+3,5-5,2+6,5-4,8\)
\(=6,5+3,5+1,2+6,5-4,8-5,2=10+7,7-10=7,7\)
d) \(3,21.\left(2^2-1,5\right)-2,5.2,22\)
\(=3,21.2,5-2,5.2,22=2,5.\left(3,21-2,22\right)=2,5.0,99=2,475\)

Bài 3:
a, (\(x\)+y+z)2
=((\(x\)+y) +z)2
= (\(x\) + y)2 + 2(\(x\) + y)z + z2
= \(x^2\) + 2\(xy\) + y2 + 2\(xz\) + 2yz + z2
=\(x^2\) + y2 + z2 + 2\(xy\) + 2\(xz\) + 2yz
b, (\(x-y\))(\(x^2\) + y2 + z2 - \(xy\) - yz - \(xz\))
= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y3
Đến dây ta thấy xuất hiện \(x^3\) - y3 khác với đề bài, em xem lại đề bài nhé

|\(x\)| = 1 ⇒ (|\(x\)|)2 = 1 ⇒ \(x^2\) = 1
Thay \(x^2\) = 1 vào biểu thức: M = (\(x^{2^{ }}\) + a)(\(x^2\) + b)(\(x^2\) + c) ta có:
M = (1 + a)(1 + b)(1 + c)
M = (1 + b + a + ab)(1 + c)
M = 1 + b + a + ab + c + bc + ac + abc
M = 1 + ( a + b + c) + (ab + bc + ac) + abc
M = 1 + 2 + (-5) + 3
M = (1+2+3) - 5
M = 1

|\(x\)| = 1 ⇒ \(x^2\) = 1
Thay \(x\)2 = 1 vào biểu thức M ta có:
M = (1 + a)(1 +b)(1+c)
M = ( 1 + b + a + ab)(1 + c)
M = 1 + b + a + ab + c + bc + ac + abc
M = 1 + (a+b+c) + (ab+bc + ac) + abc
M = 1 + 2 - 5 + 3
M = 1

a,
(\(x\) + y + z)2
= ((\(x\) + y) + z)2
= (\(x\)+y)2+2(\(x\)+y)z+ z2
= \(x^2\) + 2\(x\)y+ y2 + 2\(x\)z + 2yz + z2
= \(x^2\) + y2 + z2 + 2\(xy\) + 2yz + 2\(x\)z
b, (\(x\)+y+z)(\(x^2\) + y2 + z2 - \(xy\) - yz - \(x\)z)
= \(x^3\) + \(x\)y2 + \(x\)z2 - \(x^2\)y - \(x\)yz - \(x^2\)z + y\(x^2\) + y3 + yz2 - \(x\)y2 - y2z - \(xyz\) +
+ z\(x^2\) + zy2 + z3 - \(xyz\) - yz2 - \(x\)z2
= \(x^{3^{ }}\)+y3+z3 - 3\(x\)yz + (\(x\)z2 - \(x\)z2) - (\(x^2\)y- \(x^2\)y) - (\(x^2\)z - \(x^{2^{ }}\)z) + (y2\(x\) - y2\(x\)) - (y2z - y2z) + (z2y - z2y)
= \(x^3\) + y3 + z3 - 3\(xyz\)
c,
VT = (\(x\) + y + z)3
VT = (\(x\) + y)3 + 3(\(x\)+y)2z + 3(\(x\) +y)z2 + z3
VT = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 + 3(\(x\)+y)z(\(x+y+z\)) + z3
VT = \(x^3\)+ y3 + z3 + 3\(xy\)(\(x\) +y) + 3(\(x+y\))z(\(x+y+z\))
VT = \(x^3\) + y3 + z3 + 3(\(x+y\))(\(xy\) + z\(x\) + zy + z2)
VT = \(x^3\) + y3 + z3 + 3(\(x\) + y){ (\(xy+xz\)) + (zy +z2)
VT = \(x^3\) + y3 + z3 + 3(\(x\) + y){ \(x\) (y+z) + z(y+z)}
VT = \(x^3\) + y3 + z3 + 3(\(x\) + y)(y+z)(\(x+z\))
VT = VP (đpcm)
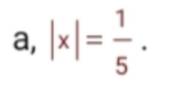
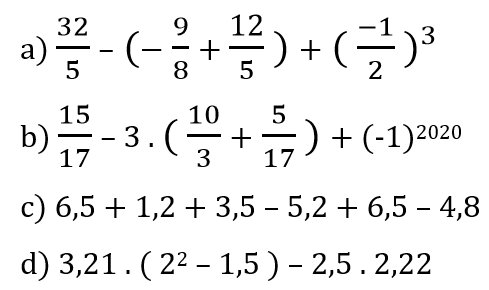

\(\widehat{xOA}=\widehat{cOA}\) (gt) (1)
\(\widehat{yOB}=\widehat{COB}\) (gt) (2)
\(\widehat{COA}+\widehat{COB}=\widehat{AOB}=90^o\) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{xOA}+\widehat{yOB}=90^o\)
\(\Rightarrow\widehat{xOy}=\widehat{COA}+\widehat{COB}+\widehat{xOA}+\widehat{yOB}=90^o+90^o=180^o\)
=> Ox và Oy là hai tia đối nhau