 giúp em giải bài này với lại cho em hỏi thêm là nếu mình gặp trường hợp căn trong căn nhưng số đằng sau là số lẻ thì mình nên nhân 2 vô hay sao ạ
giúp em giải bài này với lại cho em hỏi thêm là nếu mình gặp trường hợp căn trong căn nhưng số đằng sau là số lẻ thì mình nên nhân 2 vô hay sao ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Câu này đơn giản em tự giải
b.
Xét hai tam giác OIM và OHN có:
\(\left\{{}\begin{matrix}\widehat{OIM}=\widehat{OHN}=90^0\\\widehat{MON}\text{ chung}\\\end{matrix}\right.\) \(\Rightarrow\Delta OIM\sim\Delta OHN\left(g.g\right)\)
\(\Rightarrow\dfrac{OI}{OH}=\dfrac{OM}{ON}\Rightarrow OI.ON=OH.OM\)
Cũng từ 2 tam giác đồng dạng ta suy ra \(\widehat{OMI}=\widehat{ONH}\)
Tứ giác OAMI nội tiếp (I và A cùng nhìn OM dưới 1 góc vuông)
\(\Rightarrow\widehat{OAI}=\widehat{OMI}\)
\(\Rightarrow\widehat{OAI}=\widehat{ONH}\) hay \(\widehat{OAI}=\widehat{ONA}\)
c.
Xét hai tam giác OAI và ONA có:
\(\left\{{}\begin{matrix}\widehat{OAI}=\widehat{ONA}\left(cmt\right)\\\widehat{AON}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAI\sim\Delta ONA\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{ON}=\dfrac{OI}{OA}\Rightarrow OI.ON=OA^2=OC^2\) (do \(OA=OC=R\))
\(\Rightarrow\dfrac{OC}{ON}=\dfrac{OI}{OC}\)
Xét hai tam giác OCN và OIC có:
\(\left\{{}\begin{matrix}\dfrac{OC}{ON}=\dfrac{OI}{OC}\\\widehat{CON}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OCN\sim\Delta OIC\left(g.g\right)\)
\(\Rightarrow\widehat{OCN}=\widehat{OIC}=90^0\) hay tam giác ACN vuông tại C
\(\widehat{ABC}\) là góc nt chắn nửa đường tròn \(\Rightarrow BC\perp AB\)
Áp dụng hệ thức lượng trong tam giác vuông ACN với đường cao BC:
\(BC^2=BN.BA=BN.2BH=2BN.BH\) (1)
O là trung điểm AC, H là trung điểm AB \(\Rightarrow OH\) là đường trung bình tam giác ABC
\(\Rightarrow OH=\dfrac{1}{2}BC\)
Xét hai tam giác OHN và EBC có:
\(\left\{{}\begin{matrix}\widehat{OHN}=\widehat{EBC}=90^0\\\widehat{ONH}=\widehat{ECB}\left(\text{cùng phụ }\widehat{IEB}\right)\end{matrix}\right.\) \(\Rightarrow\Delta OHN\sim\Delta EBC\left(g.g\right)\)
\(\Rightarrow\dfrac{OH}{EB}=\dfrac{HN}{BC}\Rightarrow HN.EB=OH.BC=\dfrac{1}{2}BC^2\)
\(\Rightarrow BC^2=2HN.EB\) (2)
(1);(2) \(\Rightarrow BN.BH=HN.BE\)
\(\Rightarrow BN.BH=\left(BN+BH\right).BE\)
\(\Rightarrow\dfrac{1}{BE}=\dfrac{BN+BH}{BN.BH}=\dfrac{1}{BH}+\dfrac{1}{BN}\) (đpcm)

Đề bài là sao nhỉ? Em có nhầm lẫn chỗ nào không? Vì đề đã cho sẵn người 1 làm riêng trong 8 giờ xong và người 2 làm riêng trong 12 giờ xong nên đó chính là đáp số rồi.

Trình bày ngắn gọn hướng giải, chi tiết tỉ mỉ em tự thực hiện
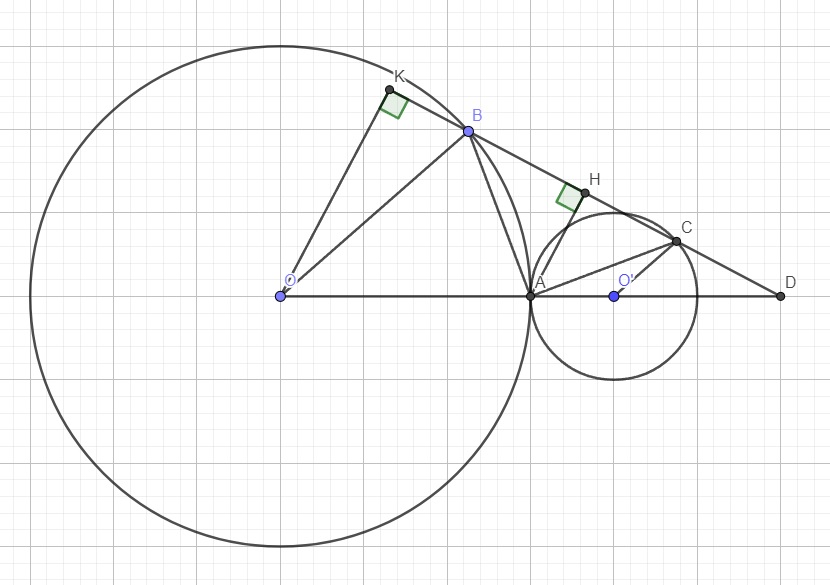
a.
AD vuông góc MO tại H \(\Rightarrow HA=HD\)
\(\Rightarrow\Delta_{\perp}OHA=\Delta_{\perp}OHD\left(c.g.c\right)\)
\(\Rightarrow\widehat{HOA}=\widehat{HOD}\)
\(\Rightarrow\Delta MOA=\Delta MOD\left(c.g.c\right)\)
\(\Rightarrow\widehat{MDO}=\widehat{MAO}=90^0\)
\(\Rightarrow MD\) là tiếp tuyến
b.
\(\widehat{MAB}=\widehat{MCA}\) (góc nt và góc tạo bởi tiếp tuyến - dây cung cùng chắn AB)
\(\Rightarrow\Delta MAB\sim\Delta MCA\)
\(\Rightarrow\dfrac{MA}{MC}=\dfrac{MB}{MA}\Rightarrow MA^2=MB.MC\)
Hệ thức lượng trong tam giác vuông MAO với đường cao AH:
\(MA^2=MH.MO\)
\(\Rightarrow MB.MC=MH.MO\Rightarrow\dfrac{MB}{MO}=\dfrac{MH}{MC}\)
Lại có \(\widehat{HMB}\) chung
\(\Rightarrow\Delta MHB\sim\Delta MCO\left(c.g.c\right)\)
c.
MA, MD là tiếp tuyến nên các tam giác MAO, MDO vuông
\(\Rightarrow M,A,D,O\) thuộc đường tròn đường kính MO
I là trung điểm BC \(\Rightarrow OI\perp BC\)
\(\Rightarrow\Delta MOI\) vuông tại I nên M, O, I thuộc đường tròn đường kính MO
\(\Rightarrow I,A,M,D\) cùng thuộc đường tròn đường kính MO
Hay đường tròn ngoại tiếp MAD đi qua I
d.
Kẻ tiếp tuyến tại B và C của (O) cắt nhau tại P
\(\Rightarrow\) Các tam giác PBO và PCO vuông nên P, B, C, O thuộc đường tròn đường kính OP (1)
Mặt khác OI đi qua trung điểm BC \(\Rightarrow OI\) là trung trực BC
\(PB=PC\) (hai tiếp tuyến cắt nhau), \(OB=OC=R\) nên OP là trung trực BC
\(\Rightarrow P,O,I\) thẳng hàng hay P nằm trên OI (2)
Từ câu b ta có \(\Delta MHB\sim\Delta MCO\Rightarrow\widehat{MCO}=\widehat{MHB}\)
Mà \(\widehat{MHB}+\widehat{BHO}=180^0\Rightarrow\widehat{MCO}+\widehat{BHO}=180^0\)
\(\Rightarrow BCOH\) nội tiếp hay 4 điểm B, C, O, H cùng thuộc 1 đường tròn (3)
(1);(3) \(\Rightarrow P,C,O,B,H\) cùng thuộc đường tròn đường kính PO
\(\Rightarrow\widehat{PHO}\) là góc nt chắn nửa đường tròn (do PO là đường kính)
\(\Rightarrow PH\perp OM\)
Mà \(AD\perp OM\) hay \(AH\perp OM\) theo giả thiết
\(\Rightarrow\) Đường thẳng PH trùng đường thẳng AD, hay P nằm trên đường thẳng AD (4)
(2);(4) \(\Rightarrow P\) là giao điểm của OI và AD
\(\Rightarrow P\) trùng Q
\(\Rightarrow Q\) là giao điểm 2 tiếp tuyến tại B và C
Hay QB, QC là tiếp tuyến của (O)

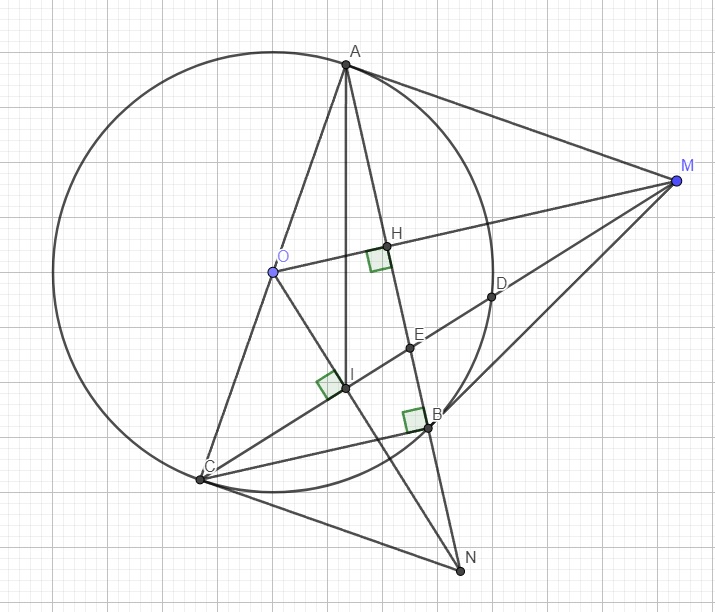
a.
OB song song O'C \(\Rightarrow\widehat{BOA}+\widehat{CO'A}=180^0\) (hai góc trong cùng phía)
Do \(OA=OB=R\) và \(O'A=O'C=R'\) nên các tam giác OAB và O'AC cân tại O và O'
\(\Rightarrow\left\{{}\begin{matrix}\widehat{OAB}=\widehat{OBA}\\\widehat{O'AC}=\widehat{O'CA}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\widehat{OAB}=\dfrac{180^0-\widehat{BOA}}{2}\\\widehat{O'AC}=\dfrac{180^0-\widehat{CO'A}}{2}\end{matrix}\right.\)
\(\Rightarrow\widehat{BAC}=180^0-\left(\widehat{OAB}+\widehat{O'AC}\right)=180^0-\left(\dfrac{180^0-\widehat{BOA}}{2}+\dfrac{180^0-\widehat{CO'A}}{2}\right)\)
\(=180^0-\left(180^0-\dfrac{\widehat{BOA}+\widehat{CO'A}}{2}\right)=90^0\)
\(\Rightarrow\Delta ABC\) vuông tại A
b.
TH1:
Nếu \(R=R'\) thì OBCO' là hình bình hành (cặp cạnh đối OB, O'C song song và bằng nhau)
\(\Rightarrow BC||O'O\Rightarrow AH\perp O'O\)
Từ B kẻ \(BK\perp O'O\Rightarrow AHBK\) là hình chữ nhật (tức giác có 3 góc vuông)
\(\Rightarrow AH=BK\le OB=R=R'\)
Dấu "=" xảy ra khi K trùng O hay BC vuông góc OB \(\Rightarrow BC\) là tiếp tuyến của (O)
TH2:
Nếu \(R\ne R'\), không mất tính tổng quát giả sử \(R>R'\)
Kéo dài BC và O'O cắt nhau tại D
Từ O kẻ \(OK\perp BC\)
Áp dụng định lý Talet: \(\dfrac{DO'}{DO}=\dfrac{OC'}{OB}=\dfrac{R'}{R}\)
OK và AH cùng vuông góc BC \(\Rightarrow OK||AH\)
Áp dụng định lý Thales:
\(\dfrac{AH}{OK}=\dfrac{DO'}{DO}=\dfrac{R'}{R}\Rightarrow AH=\dfrac{R'}{R}.OK\)
\(\Rightarrow AH_{max}\) khi \(OK_{max}\)
Mà \(OK\perp BC\Rightarrow OK\le OB\) (đường vuông góc ko lớn hơn đường xiên)
\(\Rightarrow OK_{max}=OB=R\)
\(\Rightarrow AH_{max}=\dfrac{R'}{R}.R=R'\)
Dấu "=" xảy ra khi K trùng B hay BC là tiếp tuyến của (O)

ĐKXĐ: \(x+2y\ne0\)
\(\left\{{}\begin{matrix}x-\dfrac{1}{x+2y}=\dfrac{7}{4}\\-\dfrac{5}{2}x+2+\dfrac{4}{x+2y}=-2\end{matrix}\right.\)
Đặt \(\dfrac{1}{x+2y}=z\) ta được hệ:
\(\left\{{}\begin{matrix}x-z=\dfrac{7}{4}\\-\dfrac{5}{2}x+4z=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\z=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{x+2y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\x+2y=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Gọi số học sinh lớp 9B là : \(x\) (học sinh) \(\left(x\inℕ^∗\right)\)
\(\Rightarrow\) Số học sinh lớp 9A là : \(x+10\) (học sinh)
Số cây học sinh lớp 9B trồng được : \(4x\) (cây)
Số cây học sinh lớp 9A trồng được : \(3\left(x+10\right)\) (cây)
Vì tổng số cây 2 lớp trồng được là : 275 cây
Nên ta có pt :
\(3\left(x+10\right)+4x=275\\ \Rightarrow3x+30+4x=275\\ \Rightarrow7x=245\\ \Rightarrow x=35\left(TMDK\right)\)
Vậy số HS lớp 9B là : 35 HS và lớp 9A là : 35+10=45(HS)

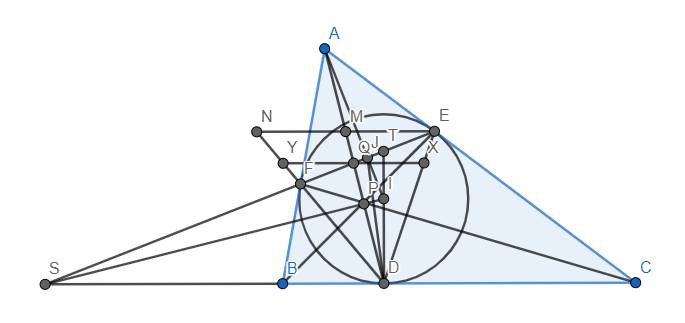
a) Do AE tiếp xúc (I) tại E nên \(\widehat{AEI}=90^o\). Đồng thời dễ dàng chứng minh \(AI\perp EF\) tại J.
Tam giác AEI vuông tại E có đường cao EJ nên \(IJ.IA=IE^2=ID^2=r^2\)
\(\Rightarrow\dfrac{IJ}{ID}=\dfrac{ID}{IA}\). Từ đó dễ có đpcm.
b) Dễ dàng chứng minh tứ giác IDSJ nội tiếp (do có \(\widehat{IJS}=\widehat{IDS}=90^o\)). Do đó \(\widehat{TIJ}=\widehat{TSD}\), dẫn đến \(\Delta TIJ~\Delta TSD\left(g.g\right)\) \(\Rightarrow\dfrac{TI}{TS}=\dfrac{TJ}{TD}\) \(\Rightarrow\) đpcm
Gọi P là giao điểm của AD và IS. Khi đó \(\widehat{PID}=\widehat{SID}=\widehat{SJD}\) và \(\widehat{PDI}=\widehat{ADI}=\widehat{IJD}\) (do đã có \(\Delta IJD~\Delta IDA\) ở câu a))
Do đó \(\widehat{PID}+\widehat{PDI}=\widehat{SJD}+\widehat{IJD}=\widehat{SJI}=90^o\)
\(\Rightarrow\Delta IPD\) vuông tại P, dẫn tới đpcm.
c) Gọi Q là giao điểm của AD và EF. Qua Q kẻ đường thẳng song song với BC cắt DE, DN lần lượt tại X, Y.
Trước hết, ta chứng minh \(\dfrac{EQ}{ES}=\dfrac{FQ}{FS}\) (*)
Ta dễ dàng chứng minh AD, BE, CF đồng quy do định lý Ceva đảo trong tam giác ABC.
\(\Rightarrow\dfrac{QF}{QE}.\dfrac{CE}{CA}.\dfrac{BA}{BF}=1\) (Ceva thuận)
Mặt khác, áp dụng định lý Menelaus cho tam giác AEF với cát tuyến SBC, ta có: \(\dfrac{SF}{SE}.\dfrac{BA}{BF}.\dfrac{CE}{CA}=1\)
Từ đó suy ra \(\dfrac{QF}{QE}=\dfrac{SF}{SE}\Rightarrow\dfrac{EQ}{ES}=\dfrac{FQ}{FS}\) . Vậy (*) được chứng minh.
Áp dụng định lý Thales \(\Rightarrow\dfrac{YQ}{SD}=\dfrac{FQ}{FS};\dfrac{XQ}{SD}=\dfrac{EQ}{ES}\)
Kết hợp với (*), ta có ngay \(YQ=XQ\), từ đó dễ dàng suy ra M là trung điểm NE dựa vào bổ đề hình thang.


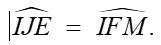
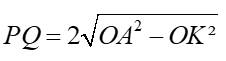
\(A=\dfrac{2\left(3+\sqrt{5}\right)}{4+\sqrt{6+2\sqrt{5}}}+\dfrac{2\left(3-\sqrt{5}\right)}{4-\sqrt{6-2\sqrt{5}}}=\dfrac{2\left(3+\sqrt{5}\right)}{4+\sqrt{\left(\sqrt{5}+1\right)^2}}+\dfrac{2\left(3-\sqrt{5}\right)}{4-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\dfrac{2\left(3+\sqrt{5}\right)}{5+\sqrt{5}}+\dfrac{2\left(3-\sqrt{5}\right)}{5-\sqrt{5}}=\dfrac{2\left(3+\sqrt{5}\right)\left(5-\sqrt{5}\right)+2\left(3-\sqrt{5}\right)\left(5+\sqrt{5}\right)}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)
\(=\dfrac{40}{20}=2\)