Ai giúp tui vs

A = 2 + 2² + 2³ + .. + 2²⁰²⁴

A = 2¹ + 2² + 2³ + ... + 2²⁰²⁴

Xét dãy số 1; 2; 3; ...; 2024, đây là dãy số cách đều với khoảng cách là: 2 - 1= 1

Số số hạng của dãy số là: (2024 - 1) : 1+  1 = 2024

Vì 2024 : 4 = 506 

Vậy nhóm 4 số hạng liên tiếp của A vào nhau ta được:

A = (2 + 2² + 2³ + 2⁴) + .. + (2²⁰²¹+ 2²⁰²² + 2²⁰²³ + 2²⁰²⁴)

A = (2 + 2² + 2³ + 2⁴) + ... + 2²⁰²⁰.(2 + 2² + 2³ + 2⁴)

A = (2 + 2² + 2³ + 2⁴).(2⁰ + ... + 2²⁰²⁰)

A = (2+ 4 +8+  16).(2⁰ + ... + 2²⁰²⁰)

A = 30.(2⁰ + ...+ 2²⁰²⁰) = 10.3.(2⁰+ ...+ 2²⁰²⁰) ⋮ 10 (đpcm)

đây là toán lớp 6 nha bn

a mk chịu

b

vì 2n-3 : 2n+2

suy ra 2(2n-3) : 2n+2

       4n-6: 2n+2

mà 2(2n+2):2n+2

     4n+4  :2n+2

    4n+ 4 -(4n-6) : 2n+2

.còn lại tự tính

ta có 4n+ 7 chia hết cho 2n +1 (1)
2n+ 1 chia hết cho 2n+1
=> 2(2n+1) chia hết cho 2n+1
=> 4n+2 chia hết cho 2n+1 (2)
từ (1) và (2)

a: \(\left(-\dfrac{1}{3}\right)^2\cdot\sqrt{81}+\left|-2023\right|\)

\(=\dfrac{1}{9}\cdot9+2023\)

=1+2023

=2024

b: \(-\dfrac{5}{11}+\dfrac{2}{7}+\dfrac{-6}{11}+\dfrac{12}{7}+4\cdot3^2\)

\(=\left(-\dfrac{5}{11}-\dfrac{6}{11}\right)+\left(\dfrac{2}{7}+\dfrac{12}{7}\right)+4\cdot9\)

\(=-1+2+36=36+1=37\)

c: \(\dfrac{3}{7}\cdot\dfrac{4}{5}+\dfrac{3}{7}\cdot\dfrac{9}{5}-\dfrac{3}{7}\cdot\dfrac{8}{5}\)

\(=\dfrac{3}{7}\left(\dfrac{4}{5}+\dfrac{9}{5}-\dfrac{8}{5}\right)\)

\(=\dfrac{3}{7}\cdot\dfrac{5}{5}=\dfrac{3}{7}\)

vì 2023+4^x = 2027 => 4^x = 2027 - 2023 => 4^x = 4 => x = 1

2023 + 4\(^{x-4}\) = 2027

            4\(^{x-4}\) = 2027 - 2023

           4\(^{x-4}\) = 4

            4\(^{x-4}\) = 4¹

             \(x-4\) = 1

                \(x=1+4\)

               \(x=5\)

Vậy \(x=5\) 

Đây là toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp đánh giá như sau: 

                            Giải: 

                       3\(^{x+1}\) = 4\(^{x-1}\) 

Vì 3 là số lẻ nên 3\(^{x-1}\) là số lẻ \(\forall\) \(x\) \(\in\) N; ⇒ 4^\(x-1\) là số lẻ

 ⇒ 4\(^{x-1}\) = 1 ⇒ 4^\(x-1\) = 4⁰ ⇒ \(x-1\) = 0⇒ \(x=1\) 

Với \(x\) = 1 ta có: 3¹⁺¹ = 4^1-1 ⇒ 3² = 4⁰ ⇒ 9 = 1 (vô lý)

Vậy \(x\) = 1 loại

Kết luận không có giá trị nào của \(x\) là số tự  nhiên thỏa mãn đề bài. 

x= 1 loại

cho mình tích được ko?

Là hình chữ nhật và có hai mặt đáy là hình tứ giác.

     Hình lăng trụ tứ giác đều là hình đa diện có hai mặt đáy là hai hình vuông bằng nhau và hai mặt đáy nằm trên hai mặt phẳng song song, các mặt bên là các hình chữ nhật. Tất cả các mặt bên đều song song và bằng nhau đồng thời vuông góc với mặt đáy. 

C = \(\dfrac{x+4}{x-1}\) (\(x\) ≠ 1) ⇒ C = 1 + \(\dfrac{5}{x-1}\)

C nguyên Dương khi và chỉ khi: 5 ⋮ \(x-1\) và \(\dfrac{x+4}{x-1}\) > 0

  5 ⋮ \(x\) - 1  ⇒ \(x-1\) \(\in\) Ư(5) = {-5; -1; 1; 5}

Lập bảng ta có:

Theo bảng trên ta có các giá trị nguyên dương của C là: 6; 2 

Kết luận các giá trị nguyên dương của C là 6 và 2

help me

  2\(\dfrac{4}{5}\) + (- \(\dfrac{3}{7}\) + \(\dfrac{2}{3}\)) : - \(\dfrac{5}{14}\)

= \(\dfrac{14}{5}\) + (\(\dfrac{-9}{21}\) + \(\dfrac{14}{21}\)) : - \(\dfrac{5}{14}\)

= \(\dfrac{14}{5}\) + \(\dfrac{5}{21}\)  x (- \(\dfrac{14}{5}\))

=  \(\dfrac{14}{5}\) - \(\dfrac{2}{3}\)

= \(\dfrac{42}{15}\) - \(\dfrac{10}{15}\)

= \(\dfrac{32}{15}\) 

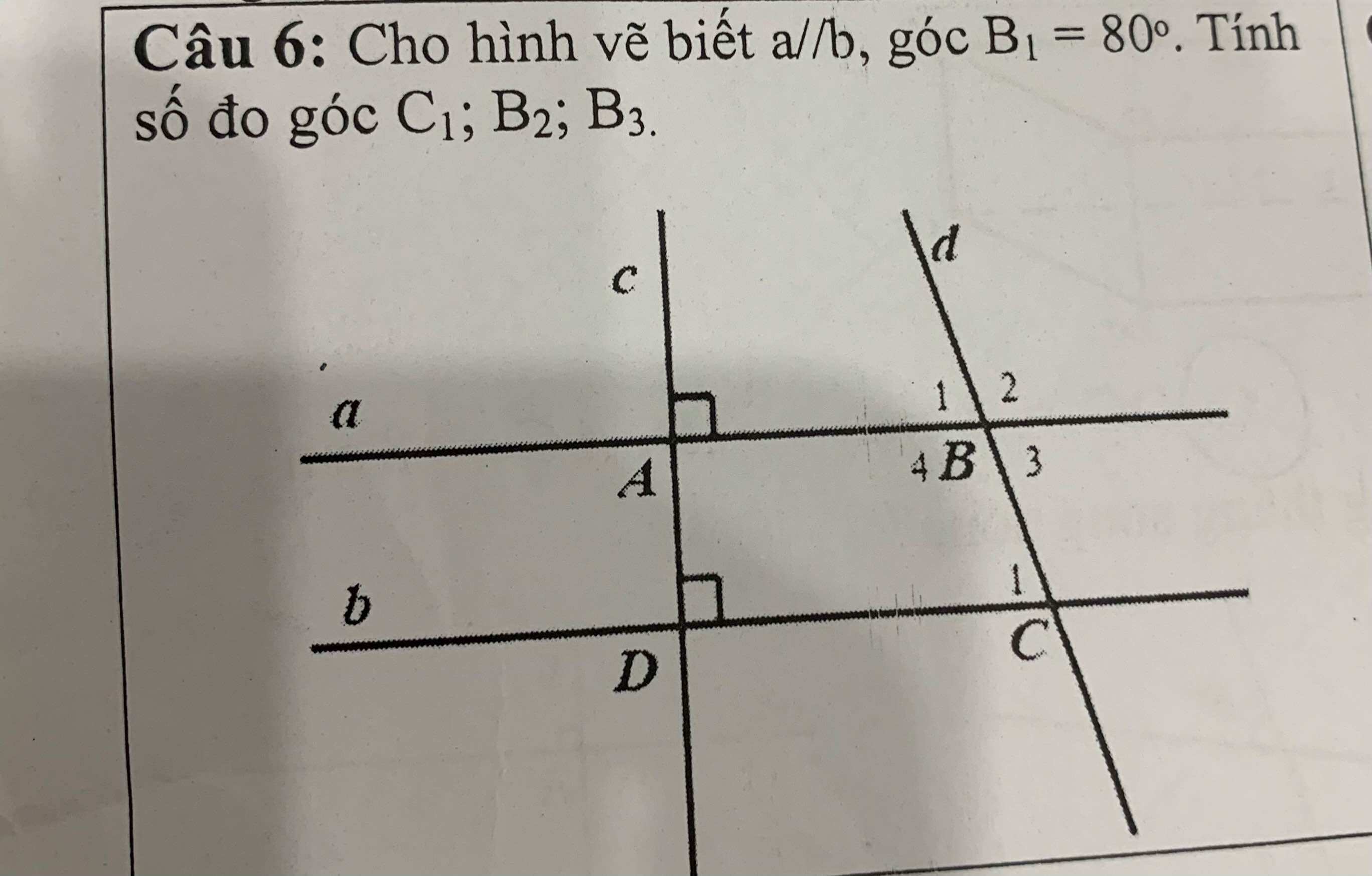
Ta có: \(\widehat{B_1}=\widehat{B_3}\)(hai góc đối đỉnh)

mà \(\widehat{B_1}=80^0\)

nên \(\widehat{B_3}=80^0\)

Ta có: \(\widehat{B_1}+\widehat{B_2}=180^0\)(hai góc kề bù)

=>\(\widehat{B_2}=180^0-80^0=100^0\)

Ta có: a//b

=>\(\widehat{C_1}=\widehat{B_3}\)(hai góc so le trong)

=>\(\widehat{C_1}=80^0\)

- \(\dfrac{11}{24}\) : \(\dfrac{17}{23}\) - \(\dfrac{11}{24}\) : \(\dfrac{17}{11}\) - \(\dfrac{1}{2}\)

= - \(\dfrac{11}{24}\) x \(\dfrac{23}{17}\) - \(\dfrac{11}{24}\) x \(\dfrac{11}{17}\) - \(\dfrac{1}{2}\)

= - \(\dfrac{11}{24}\) x (\(\dfrac{23}{17}\) + \(\dfrac{11}{17}\)) - \(\dfrac{1}{2}\)

= - \(\dfrac{11}{24}\) x 2 - \(\dfrac{1}{2}\)

= - \(\dfrac{11}{12}\) - \(\dfrac{1}{2}\)

 = - \(\dfrac{11}{12}\) - \(\dfrac{6}{12}\)

= - \(\dfrac{17}{12}\)