27 mũ 4 nhân 81 mũ 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{3x+2}{3}=\dfrac{-4}{5}\\ =>5\left(3x+2\right)=-4\cdot3\\ =>5\left(3x+2\right)=-12\\ =>3x+2=-\dfrac{12}{5}\\ =>3x=-\dfrac{12}{5}-2\\ =>3x=-\dfrac{22}{5}\\ =>x=\dfrac{-22}{5}:3\\ =>x=\dfrac{-22}{15}\)

Gọi các số nguyên tố liên tiếp tăng dần là \(p_1,p_2,p_3,...\) với \(p_1=2,p_2=3,p_3=5,...\)
Giả sử tồn tại \(m>1\) để với mọi \(n\inℕ^∗\) thì \(p_{n+1}-p_n\le m\) hay \(p_n\ge p_{n+1}-m\)
Khi đó, với mọi \(n\inℕ^∗\) thì:
\(p_1\ge p_2-m\ge p_3-2m\ge...\ge p_{n+1}-nm\)
Suy ra \(p_{n+1}\ge mn+2\) hay \(m\le\dfrac{p_{n+1}-2}{n}\) với mọi \(n\inℕ^∗\). Tuy nhiên, nếu cho \(n=1\) thì \(m\le\dfrac{p_2-2}{1}=1\), vô lý vì \(m>1\).
Vậy điều giả sử là sai \(\Rightarrow\) đpcm.
ý tưởng chứng minh bằng phản chứng của anh Lê Song Phương rất hay. Tuy nhiên, đề bài cần chứng minh là:
\(\forall m>1,m\inℕ,\exists n\inℕ\) sao cho \(p_{n+1}-p_n>m\)
Nếu nhìn kỹ hơn thì đề bài có thể mở rộng thêm 1 chút
\(\forall m\inℕ,\exists n\inℕ\) sao cho \(p_{n+1}-p_n>m\)

1) 15.9^3 : 27 - 6^2.12 +18.41
= 15.729 : 27 - 36.12 +738
= 10935 : 27 - 432 + 738
= 405 - 432 + 738
= 711
2) 18.7^3 + 9.2^6 :8 - 12.7
= 18.343 + 9.64 :8 - 84
= 6174 + 72 - 84
= 6162
3) 23.2^5 + 288.4^2 :12
= 23.32 + 288.16 :12
= 736 + 384
= 1120
4) 12^2 : 36 + 8^2 : 4 - 5.3
= 144 : 36 + 64 : 4 - 15
= 4 + 16 - 15
= 5

a) \(\left(x+3\right)\cdot\left(y+2\right)=1\) (1)
Vì x,y nguyên nên x+3;y+2 cũng nguyên (2)
Từ (1) và (2) suy ra:
\(\left(x+3\right);\left(y+2\right)\inƯ\left(1\right)=\left\{1;-1\right\}\)
Ta có bảng sau:
| x+3 | 1 | -1 |
| y+2 | 1 | -1 |
| x | -2 | -4 |
| y | -1 | -3 |
| Thoả mãn | Thoả mãn |
Vậy...
b) \(\left(2x-5\right)\cdot\left(y-6\right)=17\) (1)
Vì x,y nguyên nên 2x-5;y-6 cũng nguyên (2)
Từ (1) và (2) suy ra:
\(\left(2x-5\right);\left(y-6\right)\inƯ\left(17\right)=\left\{1;-1;17;-17\right\}\)
Ta có bảng sau:
| 2x-5 | 1 | 17 | -1 | -17 |
| y-6 | 17 | 1 | -17 | -1 |
| x | 3 | 11 | 2 | -6 |
| y | 23 | 7 | -11 | 5 |
| Thoả mãn | Thoả mãn | Thoả mãn | Thoả mãn |
Vậy....
c) \(\left(x-1\right)\left(x+y\right)=33\) (1)
Vì x,y nguyên nên x-1;x+y cũng nguyên (2)
Từ (1) và (2) suy ra:
\(\left(x-1\right);\left(x+y\right)\inƯ\left(33\right)=\left\{1;-1;3;-3;11;-11;33;-33\right\}\)
Ta có bảng sau:
| x-1 | 1 | 33 | -1 | -33 | 3 | 11 | -3 | -11 |
| x+y | 33 | 1 | -33 | -1 | 11 | 3 | -11 | -3 |
| x | 2 |
34 |
0 | -32 | 4 | 12 | -2 | -10 |
| y | 31 | -33 | -33 | 31 | 7 | -9 | -9 | 7 |
| Thoả mãn | Thoả mãn | Thoả mãn | Thoả mãn | Thoả mãn | Thoả mãn | Thoả mãn | Thoả mãn |
Vậy...

\(\left(0,4-\dfrac{2}{9}+\dfrac{2}{11}\right):\left(1,4-\dfrac{7}{9}+\dfrac{7}{11}\right)\\ =\dfrac{0,4-\dfrac{2}{9}+\dfrac{2}{11}}{1,4-\dfrac{7}{9}+\dfrac{7}{11}}\\ =\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}\\ =\dfrac{2\cdot\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7\cdot\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}\\ =\dfrac{2}{7}\)

a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
b: ta có: A nằm giữa O và B
=>OA+AB=OB
=>AB+3=6
=>AB=3(cm)
ta có: A nằm giữa O và B
mà OA=AB(=3cm)
nên A là trung điểm của OB
c: Trên tia đối của tia Ax, ta có: AO<AM
nên O nằm giữa A và M
=>AO+OM=AM
=>OM+3=6
=>OM=3(cm)
=>OM=OA(=3cm)

\(x+10\%\cdot x+20\%\cdot x+30\%\cdot x=4,8\)
=>\(x\left(1+0,1+0,2+0,3\right)=4,8\)
=>\(x\cdot1,6=4,8\)
=>\(x=4.8:1.6=3\)

Số tiền Mai tiết kiệm trong 1 ngày là:
\(20000-12000-5000=3000\left(đồng\right)\)
Số tiền Mai tiết kiệm sau 15 ngày là \(3000\cdot15=45000\left(đồng\right)\)
=>Chọn B
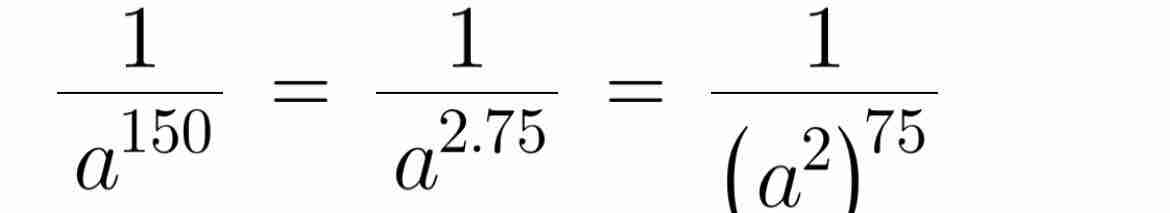
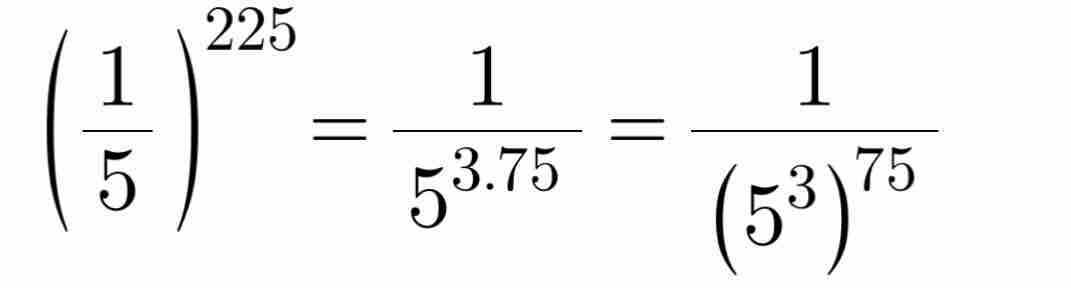
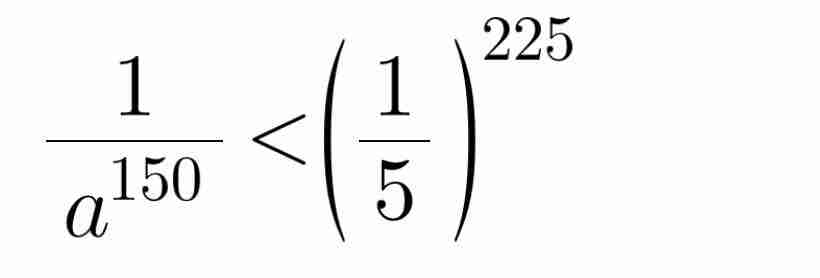
274 x 8110 = 312 x 340 = 352
274 x 8110
= (33)4 x (34)10
= 312 x 340
= 312+40
= 352