Em nên viết đề bài bằng công thức toán học có biểu tượng \(\Sigma\) góc trái màn hình.

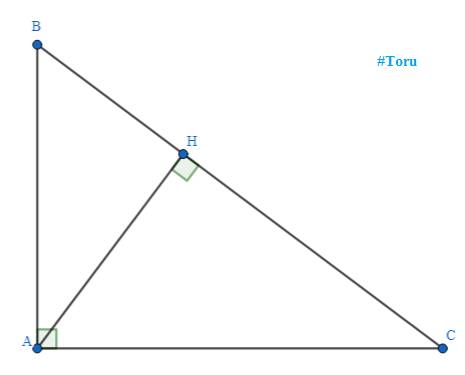
a, Xét \(\Delta HBA\) và \(\Delta ABC\) có:

\(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^{\circ}\left(AH\bot BC;\Delta ABC\text{ vuông tại }A\right)\\\widehat{ABC}\text{ chung}\end{matrix}\right.\)

\(\Rightarrow \Delta HBA\backsim \Delta ABC(g.g)\)

b, Vì \(\Delta HBA\backsim \Delta ABC(cmt)\Rightarrow \widehat{HAB}=\widehat{ACB}\) (hai góc tương ứng)

hay \(\widehat{HAB}=\widehat{HCA}\) (do \(H\in BC\)>)>

Xét \(\Delta AHB\) và \(\Delta CHA\) có: \(\left\{{}\begin{matrix}\widehat{AHB}=\widehat{CHA}=90^{\circ}\left(AH\bot BC\right)\\\widehat{HAB}=\widehat{HCA}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow \Delta AHB\backsim \Delta CHA(g.g)\Rightarrow \dfrac{AH}{CH}=\dfrac{HB}{HA}\) (các cạnh tương ứng)

\(\Rightarrow AH^2=HB\cdot HC\)

Hàm số bậc nhất có dạng: y = a\(x\) + b

Vì hệ số góc là - 3 nên a = -3 hàm số có dạng:

                      y = - 3\(x\) + b (d)

Vì hàm số cắt trục hoành tại đểm có hoành độ bằng 2 nên hàm số đó đi qua điểm A(2; 0).

Thay tọa độ điểm A vào phương trình đường thẳng d ta có 

                    -3.2 + b  = 0

                    -6 + b = 0

                            b = 6

Vậy hàm số có hệ số góc bằng -3 và cắt trục hoành có hoành độ bằng 2 có phương trình là:

                     y = -3\(x\) + 6

Đồ thị hàm số bậc nhất có dạng:

y = a\(x\) + b

Vì hệ số góc là 2 nên a = 2

Khi đó y = 2\(x\) + b (d)

Vì đồ thị đi qua điểm A(1; 2) nên tọa độ điểm A phải thỏa mãn phương trình đường thẳng (d)

Thay tọa độ điểm A(1; 2) vào (d) ta có:

2.1 + b = 2

2 + b =  2

      b = 2 - 2

      b = 0

Kết luận: Hàm số bậc nhất đi qua điểm A(1;2) và có hệ số góc là 2 là đồ thị có phương trình sau:

            y = 2\(x\) 

Gọi phương trình hàm số bậc nhất có dạng \(y=ax+b\)

Do hàm số có hệ số góc là 2 \(\Rightarrow a=2\)

\(\Rightarrow y=2x+b\)

Do đồ thị hàm số đi qua điểm có tọa độ (1;2), thay vào pt hàm số ta được:

\(2=2.1+b\Rightarrow b=0\)

Vậy hàm số có dạng: \(y=2x\)

Gọi số sản phẩm phải làm theo kế hoạch của tổ 1 là x (sản phẩm) với \(0< x< 90\)

Số sản phẩm phải làm theo kế hoạch của tổ 2 là \(90-x\) sản phẩm

Thực tế tổ 1 vượt mức 15% kế hoạch nên làm được: \(x.\left(100\%+15\%\right)=1,15x\) (sản phẩm)

Thực tế tổ 2 vượt mức kế hoạch 15% nên làm được: \(\left(90-x\right)\left(100\%+12\%\right)=1,12\left(90-x\right)\) (sản phẩm)

Do 2 tổ thực tế làm được \(90+12=102\) sản phẩm nên ta có pt:

\(1,15x+1,12\left(90-x\right)=102\)

\(\Leftrightarrow0,03x=1,2\)

\(\Leftrightarrow x=40\)

Vậy theo kế hoạc tổ 1 làm 40 sản phẩm, tổ 2 làm \(90-40=50\) sản phẩm

Để \(A=5\) thì \(\dfrac{x-2}{4}=5\)

\(\Leftrightarrow x-2=20\)

\(\Leftrightarrow x=22\)

Vậy để \(A=5\) thì \(x=22\).

Gọi x (km) là độ dài quãng đường AB (x > 0)

Thời gian đi từ A đến B: x/45 (h)

Vận tốc lúc về: 45 - 5 = 40 (km/h)

Thời gian lúc về: x/40 (h)

30 phút = 1/2 h

Theo đề bài, ta có phương trình:

x/40 - x/45 = 1/2

9x - 8x = 180

x = 180 (nhận)

Vậy quãng đường AB dài 180 km

120km

gửi nhầm

Ta có: \(A=\dfrac{3+8x}{4x^2+1}\)

Xét \(A-4=\dfrac{3+8x}{4x^2+1}-4=\dfrac{3+8x-4\left(4x^2+1\right)}{4x^2+1}\)

\(=\dfrac{-16x^2+8x-1}{4x^2+1}=\dfrac{-\left(16x^2-8x+1\right)}{4x^2+1}=\dfrac{-\left(4x-1\right)^2}{4x^2+1}\)

Ta thấy: \(\left\{{}\begin{matrix}-\left(4x-1\right)^2\le0;\forall x\\4x^2+1>0;\forall x\end{matrix}\right.\Rightarrow\dfrac{-\left(4x-1\right)^2}{4x^2+1}\le0;\forall x\)

\(\Rightarrow A-4\le0;\forall x\Rightarrow A\le4;\forall x\)

Dấu \("="\) xảy ra khi: \(4x-1=0\Leftrightarrow x=\dfrac{1}{4}\)

Vậy \(A_{max}=4\) tại \(x=\dfrac{1}{4}\).