Ba bác sĩ Xuân, Hạ, Thu cùng công tác chung ở một bệnh viện. Bác sĩ Xuấn cứ 15 ngày trực đêm một lần, bác sĩ Hạ cứ 20 ngày trực đêm một lần, bác sĩ Thu cứ 18 ngày trực đêm một lần. Lần đầu cả 3 bác sĩ cùng trực đêm chung. Hỏi ít nhất có bao nhiêu ngày nữa thì cả 3 bác sĩ cùng trực đêm chung? Tính cả lần trực đêm chung này thì mỗi bác sĩ trực bao nhiêu lần?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x\) \(\in\)N; \(x\) ⋮10; 12; 18; 0< \(x\) < 300
⇒ \(x\) \(\in\)BC(10; 12; 18)
10 = 2.5; 12 = 22.3; 18 = 2.32 BCNN(10; 12; 18) = 22.32.5 = 180
⇒ \(x\) \(\in\) {0; 180; 360;...;}
Vì 0< \(x\) < 300 ⇒ \(x\) = 180
Lời giải:
$x\vdots 10,12,18$ nên $x$ là BC(10,12,18)
$\Rightarrow x\vdots BCNN(10,12,18)$
$\Rightarrow x\vdots 180$
Mà $0< x< 300$ nên $x=180$

\(a,M=35a+70b+14=7\left(5a+10b+2\right)⋮7\left(đpcm\right)\\ b,M=5\left(7a+14b+2\right)+4\\ Mà:4⋮̸5\Rightarrow5\left(7a+14b+2\right)+4⋮̸5\\ \Rightarrow M⋮̸5\left(đpcm\right)\)

Hiệu 2 số hạng kề nhau:
8-7=1(đơn vị)
Số lượng số hạng của dãy:
(100-6):1 + 1= 95(số hạng)
Tổng trên bằng:
(100+6):2 x 95 = 5035
Đ.số: 5035

Khoảng cách : `4`
Số số hạng là : \(\dfrac{201-1}{4}+1=51\)
Tổng là : \(\dfrac{\left(201+1\right)\cdot51}{2}=5151\)
A = 1 + 5 + 9 + 13 +...+ 201
Dãy số trên là dãy số cách đều với khoảng cách là 5 - 1 = 4
Số số hạng của dãy số trên là: (201 -1):4 + 1 = 51
Tổng dãy trên là: (201 +1) x 51: 2 = 5151

Độ dài tất cả các cạnh là: 4 x 6 = 24 (cm)
Độ dài tất cả các đường chéo là: 8 x 3 = 24 (cm)
Tổng độ dài tất cả các cạnh và các đường chéo là:
24 + 24 = 48 (cm)
Kết luận

\(a,Ư\left(70\right)=\left\{1;2;5;7;10;14;35;70\right\}\\ B\left(7\right)=\left\{0;7;14;21;28;35;42;49;56;63;72;81;90;99;....\right\}\\ \Rightarrow n\in\left\{7;14;35;70\right\}\\ b,Ư\left(225\right)=\left\{1;3;5;9;15;25;45;75;225\right\}\\ B\left(9\right)=\left\{0;9;18;27;36;45;54;63;72;81;...;216;225;234;243;...\right\}\\ \Rightarrow n\in\left\{9;45;225\right\}\)
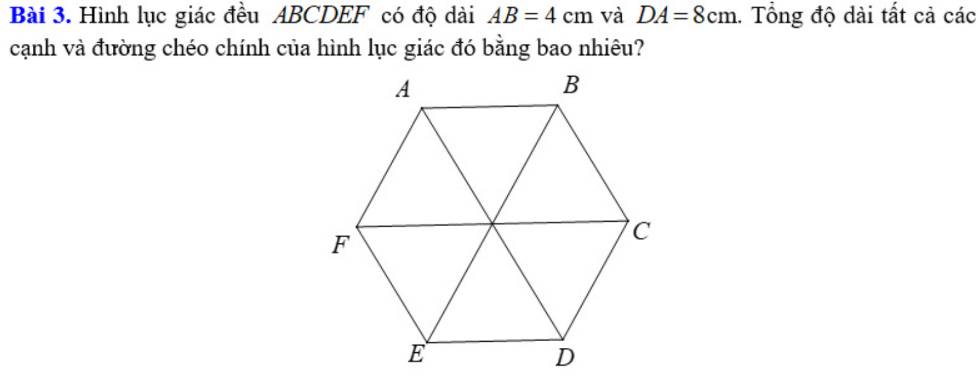
Ta có 15 = 3.5; 20 = 22.5 và 18 = 2.32
Do đó BCNN(15; 18; 20) = 22.32.5 = 180
Vậy ít nhất 180 ngày nữa thì cả 3 bác sĩ cùng trực đêm chung.
Khi đó, tính cả lần trực đêm chung này thì mỗi bác sĩ Xuân, Hạ, Thu lần lượt trực số ca là:
180 : 15 + 1 = 13 (ca)
180 : 18 + 1 = 11 (ca)
180 : 20 + 1 = 10 (ca)