Có 3 hộ dân ở 3 vị trí A, B, C tạo thành một hình tam giác. Chính quyền địa phương muốn mắc điện cho 3 hộ dân này bằng cách xây dựng một trụ điện tại một điểm P ở miền trong tam giác ABC và mắc 3 dây điện nối từ P đến A, B, C. Hỏi cần chọn P ở vị trí nào để chi phí lắp đặt dây điện là ít nhất?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a)4^7:2^5\\ =\left(2^2\right)^7:2^5\\ =2^{14}:2^5\\ =2^9\\ b)3^{10}:9^3\\ =3^{10}:\left(3^2\right)^3\\ =3^{10}:3^6\\ =3^4\\ c)27^9:3^{10}\\ \left(3^3\right)^9:3^{10}\\ =3^{27}:3^{10}\\ =3^{17}\\ d)25^5:5^3\\ =\left(5^2\right)^5:5^3\\ =5^{10}:5^3\\ =5^7\\ e)36^7:6^4\\ =\left(6^2\right)^7:6^4\\ =6^{14}:6^4\\ =6^{10}\\ g)4^3\cdot8^4\\ =\left(2^2\right)^3\cdot\left(2^3\right)^4\\ =2^6\cdot3^{12}\\ =2^{18}\)

4, Ta có \(3x=7y=42z\Leftrightarrow\dfrac{3x}{21}=\dfrac{7y}{21}=\dfrac{42z}{21}\Leftrightarrow\dfrac{x}{7}=\dfrac{y}{3}=2z\)
Đặt \(\dfrac{x}{7}=\dfrac{y}{3}=2z=k\Rightarrow x=7k;y=3k\)
Ta có \(x^2+z^2=49k^2+\dfrac{k^2}{4}=\dfrac{197}{4}k^2=197\Leftrightarrow k^2=4\Leftrightarrow k=\pm2\)
Với k = 2
\(x=14;y=6;z=1\)
Với k = -2
\(x=-14;y=-6;z=-1\)

\(\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+\dfrac{3}{10\cdot13}+...+\dfrac{3}{87\cdot90}\)
\(=\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{87}-\dfrac{1}{90}\)
\(=\dfrac{1}{4}+\left(\dfrac{1}{7}-\dfrac{1}{7}\right)+\left(\dfrac{1}{10}-\dfrac{1}{10}\right)+...+\left(\dfrac{1}{87}-\dfrac{1}{87}\right)-\dfrac{1}{90}\)
\(=\dfrac{1}{4}-\dfrac{1}{90}\)
\(=\dfrac{45}{180}-\dfrac{2}{180}\)
\(=\dfrac{43}{180}\)

Lời giải:
Áp dụng TCDTSBN:
$\frac{3x-2y}{4}=\frac{2z-4x}{3}=\frac{4y-3z}{2}$
$=\frac{4(3x-2y)}{16}=\frac{3(2z-4x)}{9}=\frac{2(4y-3z)}{4}$
$=\frac{4(3x-2y)+3(2z-4x)+2(4y-3z)}{16+9+4}=\frac{0}{29}=0$
$\Rightarrow 3x-2y=2z-4x=4y-3z=0$
$\Rightarrow 3x=2y; 2z=4x$
$\Rightarrow \frac{x}{2}=\frac{y}{3}; \frac{x}{2}=\frac{z}{4}$
$\Rightarrow \frac{x}{2}=\frac{y}{3}=\frac{z}{4}$
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$. Khi đó:
$x+2y+3z=20$
$\Rightarrow 2t+2.3t+3.4t=20$
$\Rightarrow 2t+6t+12t=20$
$\Rightarrow 20t=20\Rightarrow t=1$
Do đó:
$x=2t=2; y=3t=3; z=4t=4$


Ta có :
\(12=2^2.3\)
\(15=3.5\)
\(=>BCNN\left(12;15\right)=3.5.2^2=3.5.4=60\)
\(=>60:12=5;60:15=4\)
\(\dfrac{5}{12}=\dfrac{5.5}{12.5}=\dfrac{25}{60}\)
\(\dfrac{8}{15}=\dfrac{8.4}{15.4}=\dfrac{32}{60}\)
Vì \(25< 32\) nên
\(=>\dfrac{25}{60}< \dfrac{32}{60}\)
\(=>\dfrac{5}{12}< \dfrac{8}{15}\)
Vậy \(\dfrac{5}{12}< \dfrac{8}{15}\)
Nếu có gì sai sót thì nhớ bảo mình , mình cảm ơn!

Gọi số xe của đội thứ nhất, thứ hai, thứ ba lần lượt là x,y,z (xe)
Điều kiện: \(x,y,z\inℕ^∗\)
Ta có:
+) Vì đội thứ nhất nhiều hơn đội thứ ba là 10 xe nên:
\(x-z=10\)
+) Vì cùng một lượng hàng hóa thì số xe chở tỉ lệ nghịch với thời gian chở nên:
\(2x=2,5y=3z\Rightarrow\dfrac{2x}{30}=\dfrac{2,5y}{30}=\dfrac{3z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{12}=\dfrac{z}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau kết hợp \(x-z=10\) được:
\(\dfrac{x}{15}=\dfrac{y}{12}=\dfrac{z}{10}=\dfrac{x-z}{15-10}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}x=15\cdot2=30\\y=12\cdot2=24\\z=10\cdot2=20\end{matrix}\right.\) (thỏa mãn điều kiện)
Vậy...
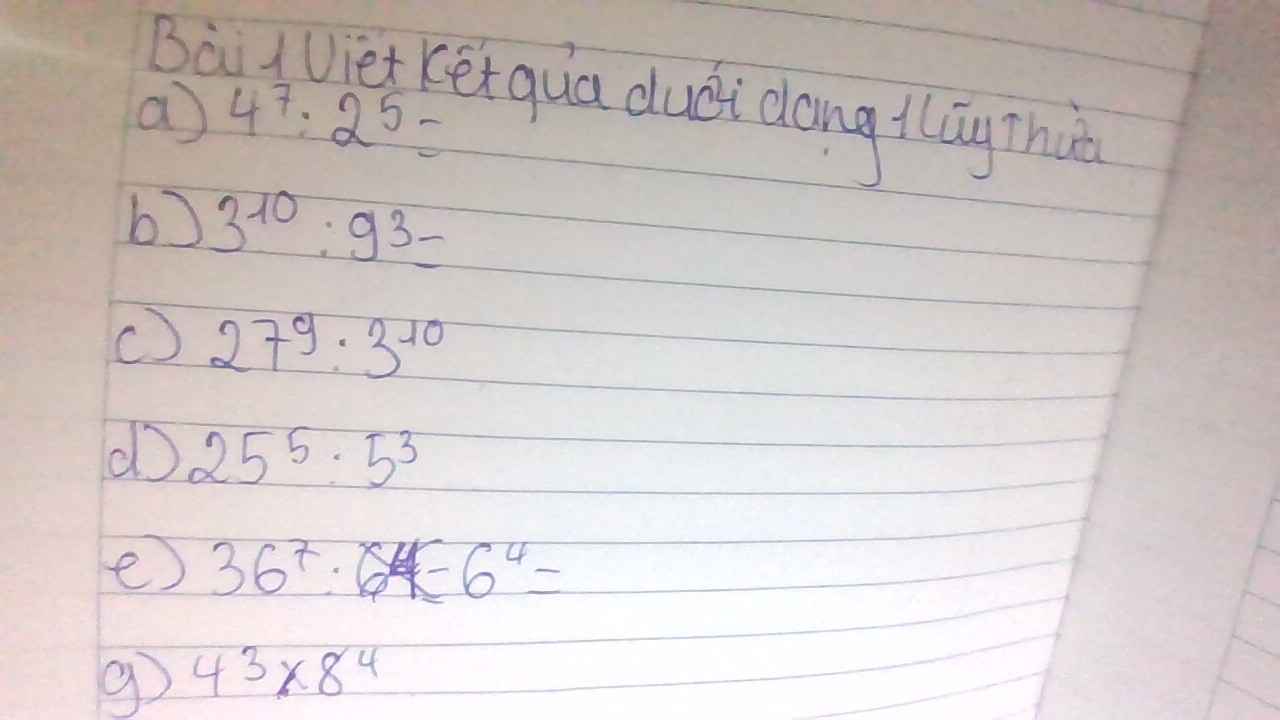

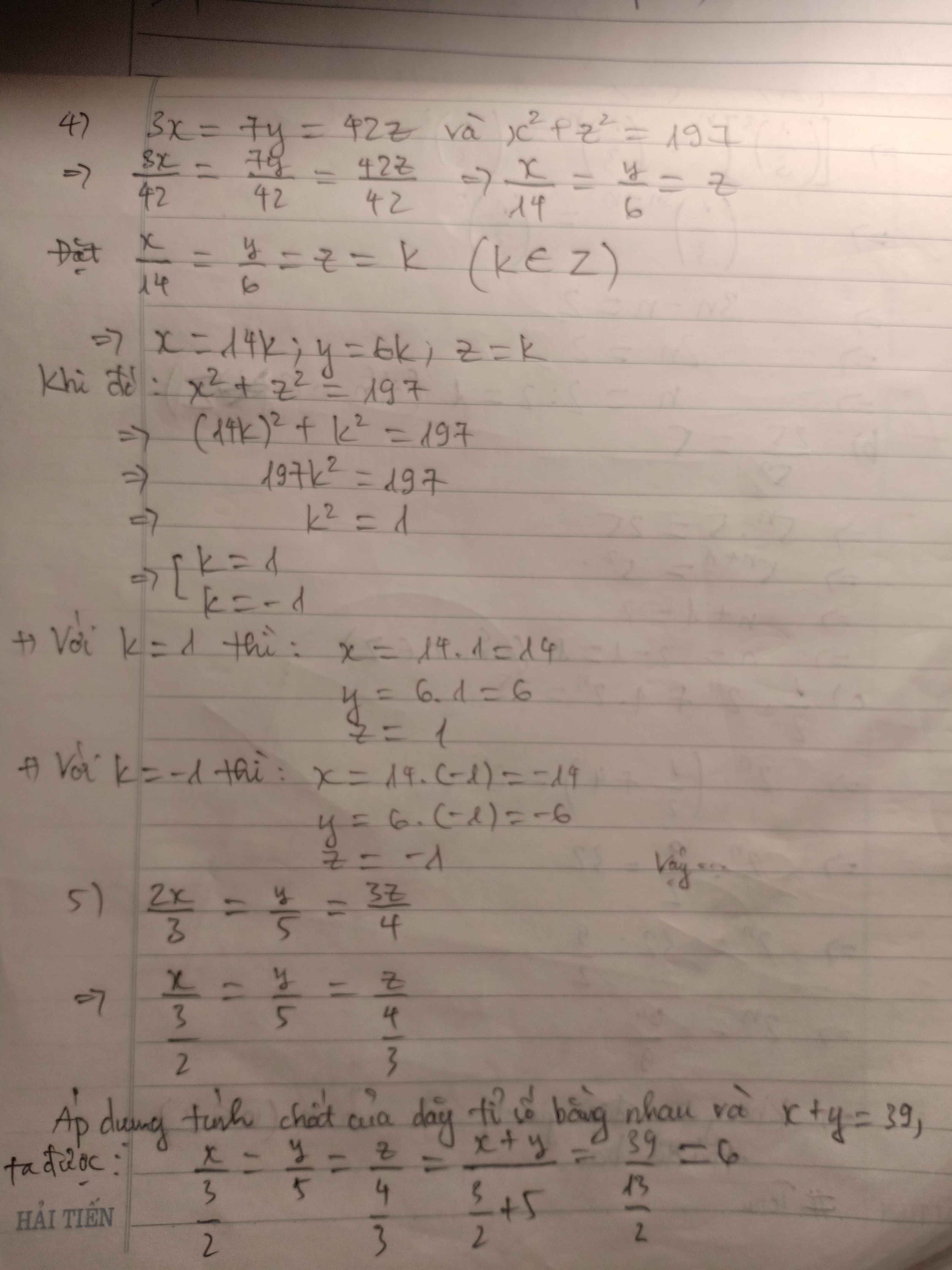
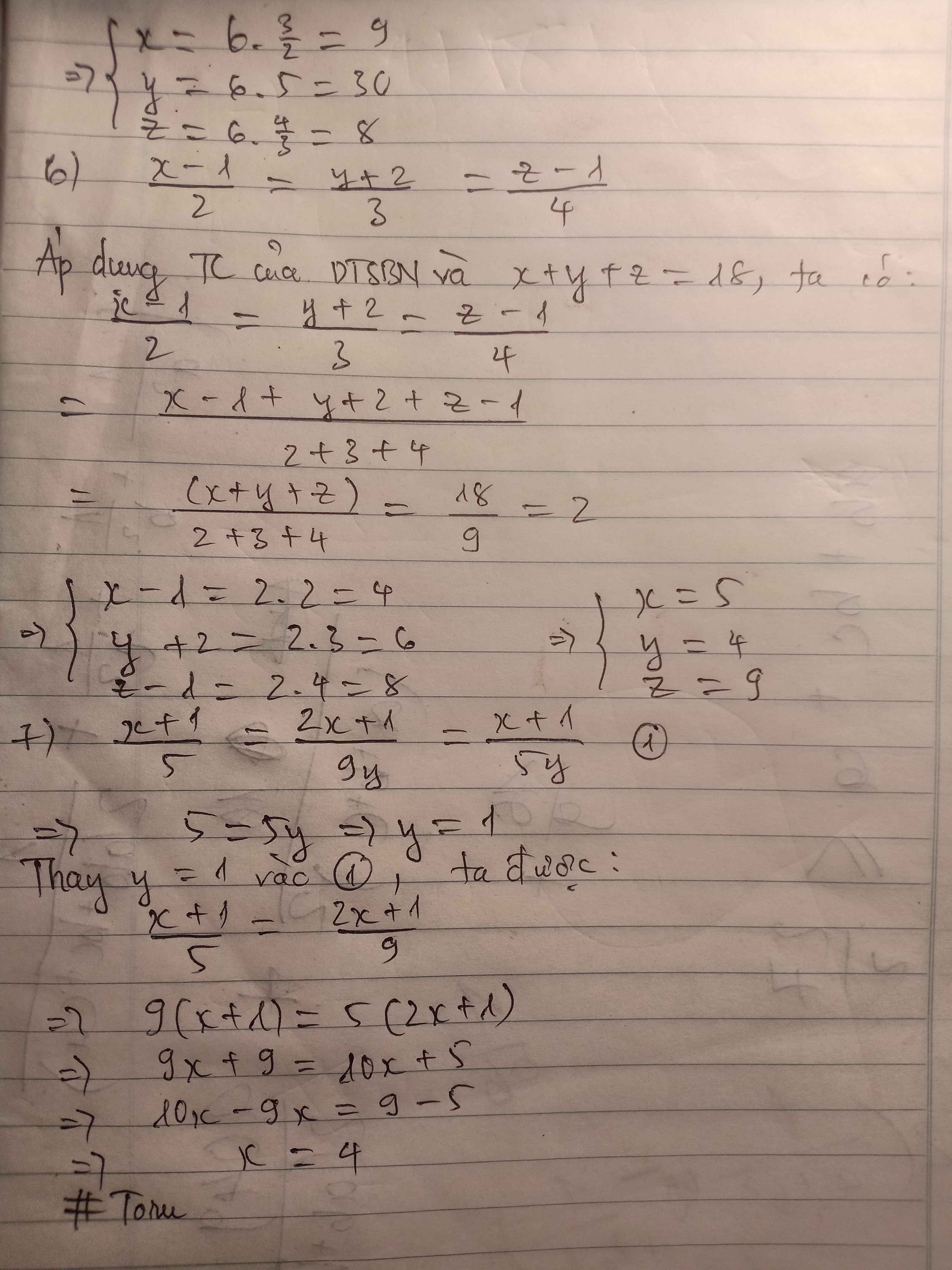
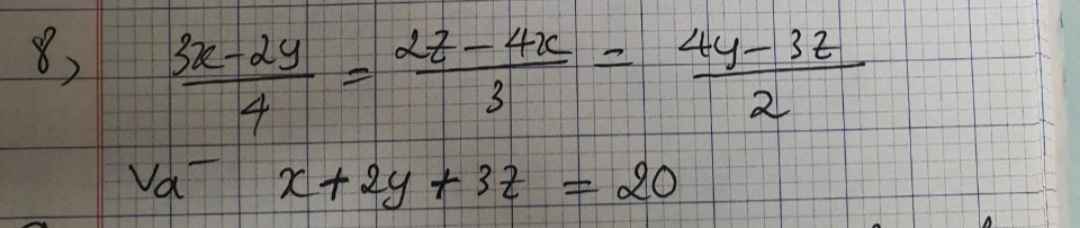
Đặt P ở trọng tâm tam giác nha. vì trọng tâm cách đều 3 đỉnh nên như thế là tiết kiệm nhất nhé
ê