\(\dfrac{1}{a^3+b^3+abc}=\dfrac{1}{\left(a+b\right)\left(a^2-ab+b^2\right)+abc}\le\dfrac{1}{\left(a+b\right)\left(2ab-ab\right)+abc}=\dfrac{1}{ab\left(a+b\right)+abc}=\dfrac{1}{ab\left(a+b+c\right)}\)
tương tự với các hạng tử còn lại, ta được
\(Vetrai\le\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\left(\dfrac{1}{a+b+c}\right)=\dfrac{a+b+c}{abc}\cdot\dfrac{1}{a+b+c}=\dfrac{1}{abc}\)
dấu bằng xảy ra khi a=b=c

Gọi x là số đo cung nhỏ AB (x > 0)

Số đo cung lớn AB là 2x

Ta có:

x + 2x = 360⁰

3x = 360⁰

x = 360⁰ : 3

x = 120⁰

⇒ ∠AOB = 120⁰

∆AOB có:

OA = OB = R

⇒ ∆AOB cân tại O

⇒ ∠OAB = ∠OBA = (180⁰ - ∠AOB) : 2

= (180⁰ - 120⁰) : 2

= 30⁰

Ta có hình vẽ sau:

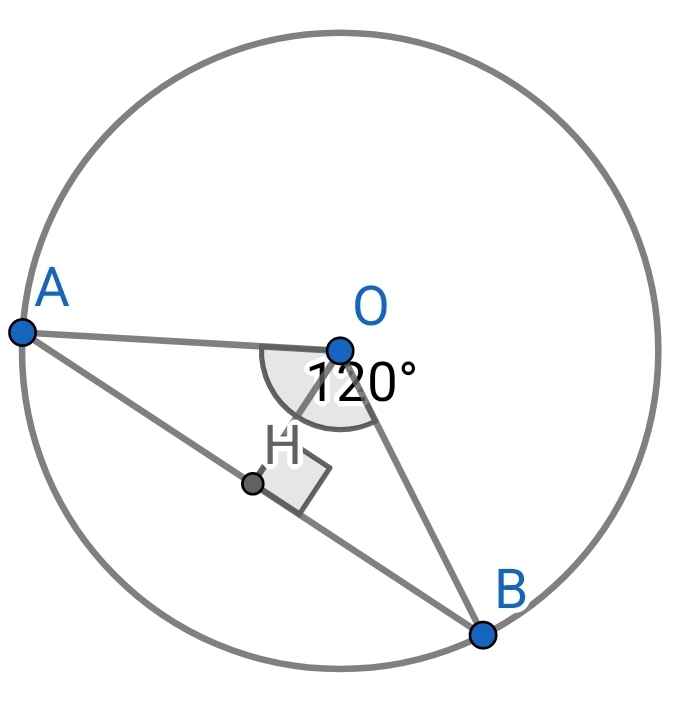
Vẽ đường cao OH của ∆OAB

⇒ ∆OAH vuông tại H

⇒ cosOAH = AH : OA

⇒ AH = OA.cosOAH

= R.cos30⁰

Do OH ⊥ AB

⇒ H là trung điểm của AB

⇒ AB = 2AH

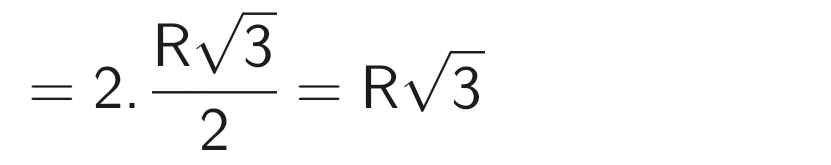
a) Gọi x là số đo cung nhỏ AB (x > 0)

Số đo cung lớn AB là 3x

Ta có:

x + 3x = 360⁰

4x = 360⁰

x = 360⁰ : 4

x = 90⁰

Vậy số đo cung nhỏ AB là 90⁰

Số đo cung lớn AB là 3.90⁰ = 270⁰

b)

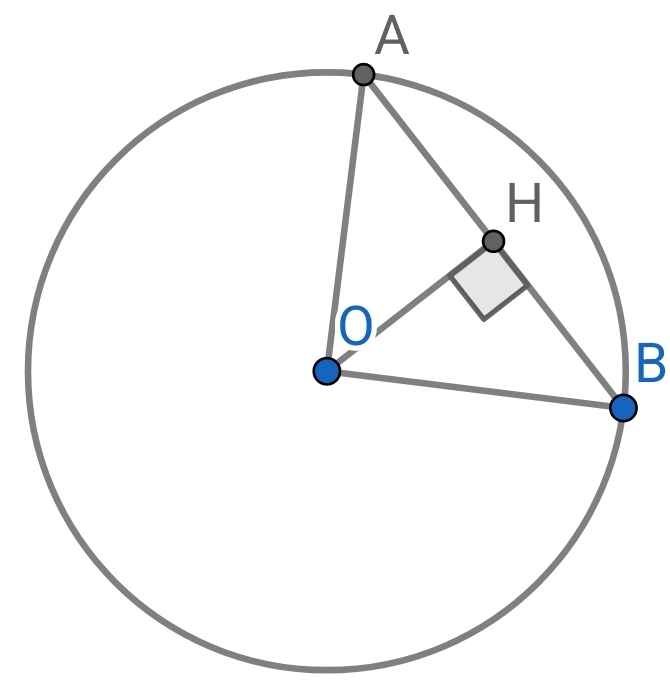
Do số đo cung nhỏ AB là 90⁰ (cmt)

⇒ ∠AOB = 90⁰

⇒ ∆AOB vuông tại O

Do OH là khoảng cách từ O đến AB

⇒ OH ⊥ AB

⇒ H là trung điểm của AB

⇒ OH là đường trung tuyến ứng với cạnh huyền AB của ∆AOB vuông tại O

⇒ OH = AB : 2

a: Xét ΔABC vuông tại C có \(sinB=\dfrac{AC}{AB}=\dfrac{a}{2a}=\dfrac{1}{2}\)

nên \(\widehat{B}=30^0\)

ΔABC vuông tại C

=>\(\widehat{CAB}+\widehat{CBA}=90^0\)

=>\(\widehat{CAB}=90^0-30^0=60^0\)

Ta có: \(\widehat{ABC}=90^0\)

=>B nằm trên đường tròn đường kính AC(1)

Ta có: \(\widehat{ADC}=90^0\)

=>D nằm trên đường tròn đường kính AC(2)

Từ (1),(2) suy ra B,D cùng nằm trên đường tròn đường kính AC

=>A,B,C,D cùng thuộc đường tròn tâm O, đường kính AC

Xét (O) có

AC là đường kính

BD là dây

Do đó: BD<AC

Xét tứ giác BC'B'C có \(\widehat{BC'C}=\widehat{BB'C}=90^0\)

nên BC'B'C là tứ giác nội tiếp đường tròn đường kính BC

=>BC'B'C là tứ giác nội tiếp đường tròn tâm O, đường kính BC

Xét (O) có

BC là đường kính

B'C' là dây

Do đó: B'C'<BC

Gọi OH là khoảng cách từ O đến dây MN

=>OH\(\perp\)MN tại H

ΔOMN cân tại O

mà OH là đường cao

nên H là trung điểm của MN

=>\(HM=HN=\dfrac{R}{2}\)

ΔOHM vuông tại H

=>\(OH^2+HM^2=OM^2\)

=>\(OH^2=R^2-\left(\dfrac{R}{2}\right)^2=\dfrac{3R^2}{4}\)

=>\(OH=\sqrt{\dfrac{3R^2}{4}}=\dfrac{R\sqrt{3}}{2}\)

=>Khoảng cách từ O đến dây MN là \(\dfrac{R\sqrt{3}}{2}\)

Gọi giao điểm của MN với OA là H

Vì MN\(\perp\)OA tại trung điểm của OA

nên MN\(\perp\)OA tại H và H là trung điểm của OA

Xét ΔOMA có 

MH là đường cao

MH là đường trung tuyến

Do đó: ΔOMA cân tại M

=>MO=MA

mà OM=OA

nên OM=MA=OA

=>ΔOMA đều

=>\(\widehat{MOA}=60^0\)

Xét ΔMHO vuông tại H có \(sinMOH=\dfrac{MH}{MO}\)

=>\(\dfrac{MH}{10}=sin60=\dfrac{\sqrt{3}}{2}\)

=>\(MH=10\cdot\dfrac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)

ΔOMN cân tại O

mà OH là đường cao

nên H là trung điểm của MN

=>\(MN=2\cdot MH=2\cdot5\sqrt{3}=10\sqrt{3}\left(cm\right)\)

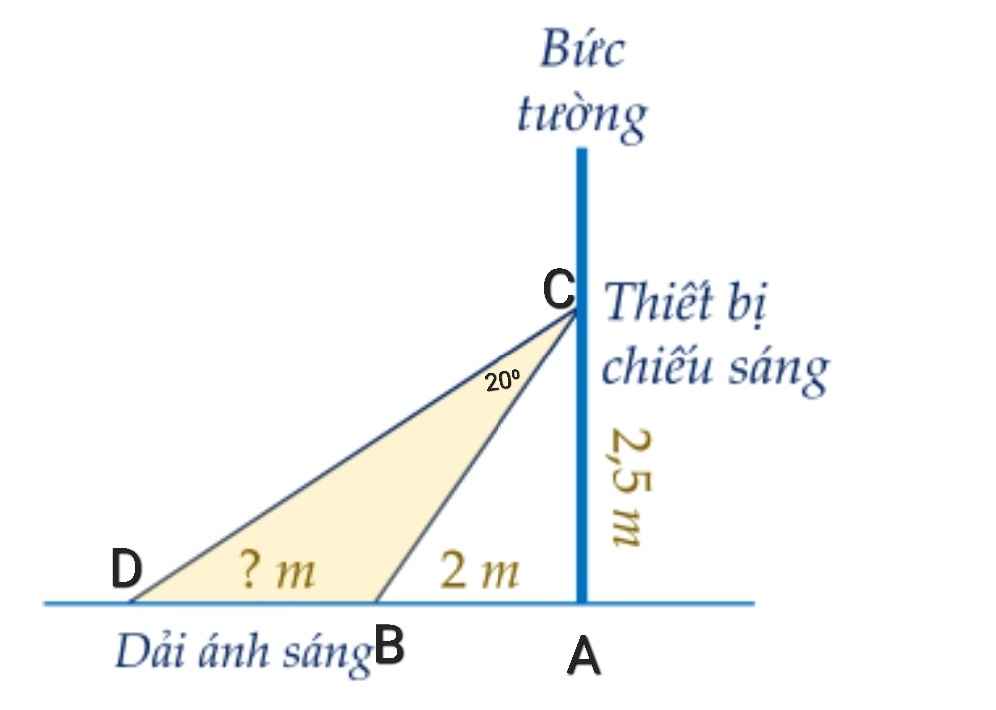
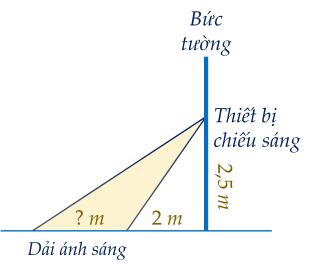
∆ABC vuông tại A

⇒ tanC = AB : AC = 2 : 2,5 = 0,8

⇒ C ≈ 39⁰

⇒ ACD = 20⁰ + 39⁰ = 59⁰

∆ACD vuông tại A

⇒ tanACD = AD : AC

⇒ AD = AC.tanACD

= 2,5.tan59⁰

≈ 4,2 (m)

Độ dài vùng được chiếu sáng trên mặt đất:

BD = AD - AB = 4,2 - 2 = 2,2 (m)

1) sin35⁰ = cos(90⁰ - 35⁰) = cos55⁰

Vậy sin35⁰ = cos55⁰

tan35⁰ = cot(90⁰ - 35⁰) = cot55⁰

Vậy tan35⁰ = cot55⁰

2) ∆ABC vuông tại A (gt)

⇒ AB = BC.cosB

= 20.cos36⁰

≈ 16,18 (cm)