 Help!
Help!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


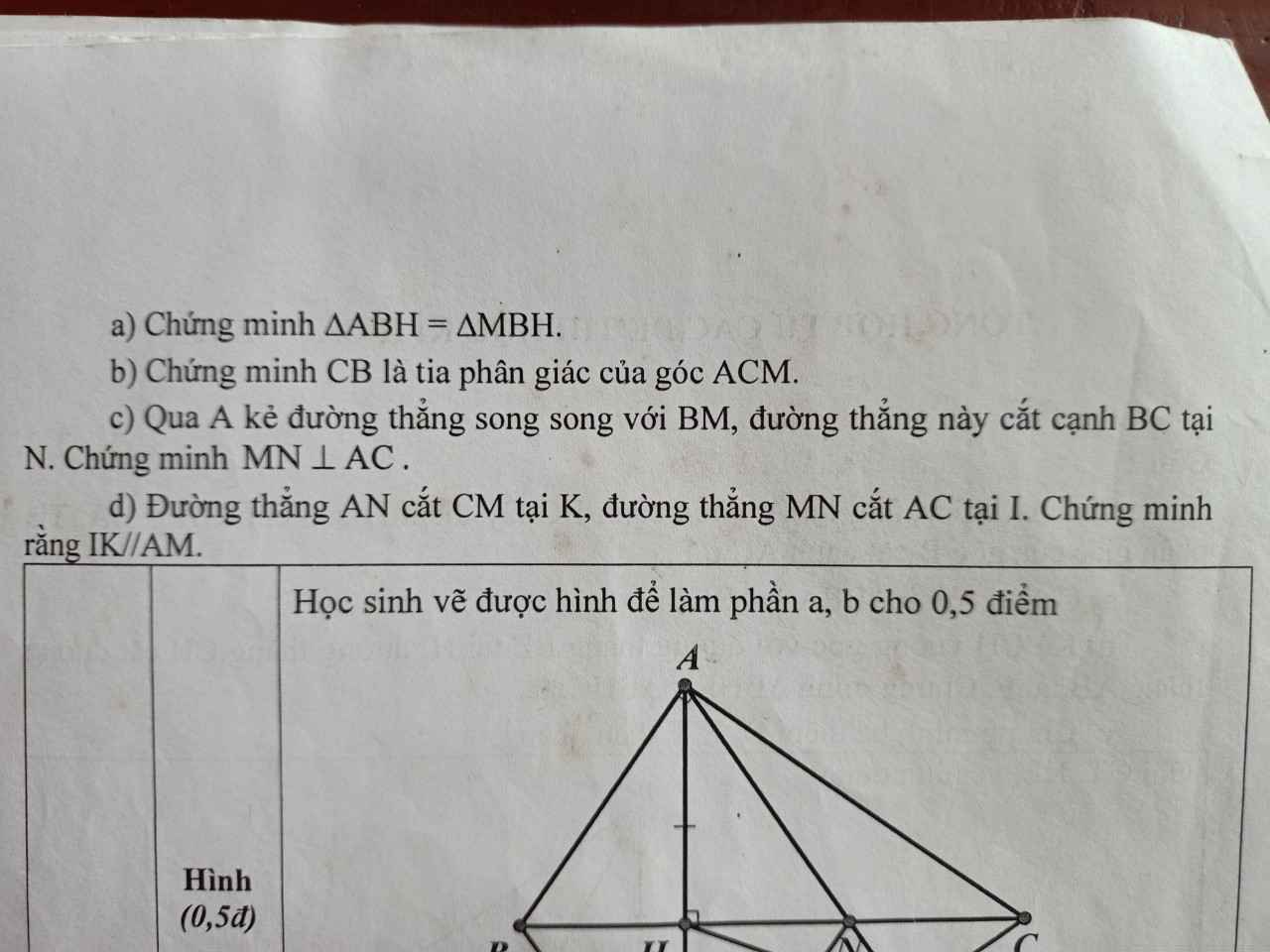
Câu 2:
a: Xét ΔBHA vuông tại H và ΔBHM vuông tại H có
BH chung
HA=HM
Do đó: ΔBHA=ΔBHM
b: ΔBHA=ΔBHM
=>BA=BM và \(\widehat{ABH}=\widehat{MBH}\)
Xét ΔBAC và ΔBMC có
BA=BM
\(\widehat{ABC}=\widehat{MBC}\)
BC chung
Do đó: ΔBAC=ΔBMC
=>\(\widehat{ACB}=\widehat{MCB}\)
=>CB là phân giác của góc ACM
c: ΔBAC=ΔBMC
=>\(\widehat{BAC}=\widehat{BMC}\)
=>\(\widehat{BMC}=90^0\)
Ta có: AN//BM
BM\(\perp\)MC
Do đó: AN\(\perp\)CM
Xét ΔCAM có
CH,AN là các đường cao
CH cắt AN tại N
Do đó: N là trực tâm của ΔCAM
=>MN\(\perp\)AC
d: ΔCAB=ΔCMB
=>CA=CM
=>ΔCAM cân tại C
Xét ΔCKA vuông tại K và ΔCIM vuông tại I có
CA=CM
\(\widehat{ACK}\) chung
Do đó: ΔCKA=ΔCIM
=>CI=CK
Xét ΔCAM có \(\dfrac{CI}{CA}=\dfrac{CK}{CM}\)
nên IK//AM


a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BC
c: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA=\sqrt{5^2-3^2}=4\left(cm\right)\)
d: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
Xét ΔAEH vuông tại E và ΔAKH vuông tại K có
AH chung
\(\widehat{EAH}=\widehat{KAH}\)
Do đó: ΔAEH=ΔAKH
=>HE=HK
e: ΔAEH=ΔAKH
=>AE=AK
Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AK}{AC}\)
nên EK//BC

Bài 3: Gọi H là giao điểm của CD với AB
\(\widehat{HCB}+\widehat{DCB}=180^0\)(hai góc kề bù)
=>\(\widehat{HCB}+143^0=180^0\)
=>\(\widehat{HCB}=180^0-143^0=37^0\)
Xét ΔHCB có \(\widehat{HCB}+\widehat{HBC}=37^0+53^0=90^0\)
nên ΔHCB vuông tại H
=>CD\(\perp\)AB tại H
Bài 2:
a: Ta có: \(\widehat{DAB}=\widehat{xAM}\)(hai góc đối đỉnh)
mà \(\widehat{xAm}=124^0\)
nên \(\widehat{DAB}=124^0\)
Ta có: \(\widehat{DAB}+\widehat{ABC}=124^0+56^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AD//BC
=>xy//zt
b: xy//zt
=>\(\widehat{BCD}+\widehat{ADC}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{BCD}+90^0=180^0\)
=>\(\widehat{BCD}=90^0\)
Ak là phân giác của góc DAB
=>\(\widehat{DAC}=\dfrac{124^0}{2}=62^0\)
ΔDAC vuông tại D
=>\(\widehat{DAC}+\widehat{DCA}=90^0\)
=>\(\widehat{DCA}+62^0=90^0\)
=>\(\widehat{DCA}=28^0\)

Bài 3: Gọi H là giao điểm của CD với AB
\(\widehat{HCB}+\widehat{DCB}=180^0\)(hai góc kề bù)
=>\(\widehat{HCB}+143^0=180^0\)
=>\(\widehat{HCB}=180^0-143^0=37^0\)
Xét ΔHCB có \(\widehat{HCB}+\widehat{HBC}=37^0+53^0=90^0\)
nên ΔHCB vuông tại H
=>CD\(\perp\)AB tại H
Bài 2:
a: Ta có: \(\widehat{DAB}=\widehat{xAM}\)(hai góc đối đỉnh)
mà \(\widehat{xAm}=124^0\)
nên \(\widehat{DAB}=124^0\)
Ta có: \(\widehat{DAB}+\widehat{ABC}=124^0+56^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AD//BC
=>xy//zt
b: xy//zt
=>\(\widehat{BCD}+\widehat{ADC}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{BCD}+90^0=180^0\)
=>\(\widehat{BCD}=90^0\)
Ak là phân giác của góc DAB
=>\(\widehat{DAC}=\dfrac{124^0}{2}=62^0\)
ΔDAC vuông tại D
=>\(\widehat{DAC}+\widehat{DCA}=90^0\)
=>\(\widehat{DCA}+62^0=90^0\)
=>\(\widehat{DCA}=28^0\)

c; C = \(\dfrac{28^{28}+28^{24}+...+28^4+1}{28^{30}+28^{28}+...+28^2+1}\)
A = 1 + 284 + 288 + 2812 + ...2828
284A = 284 + 288 + 2812 + ... + 2828 + 2832
284A - A = 284+ 288+...+2828+ 2832- (1 + 284 + 288+...+2828)
(284 - 1)A = 284 + 288+ ...+ 2828 + 2832 - 1 - 284- ...- 2828
(284 - 1)A = (2832 - 1) + (284 - 284) + (288 - 288) + ... + (2828 - 2828)
(284 - 1)A = 2832 - 1 + 0 + 0... + 0
A = (2832 - 1): (284 - 1)
Đặt B = 2830 + 2828 + ... + 282 + 1
282B = 2832 + 2830 + ... + 284 + 282
282B - B = 2832 + 2830 + ... + 284 + 282 - (2830 + 2828 +...+1)
(282 - 1)B = 2832 + 2830+...+284 + 282 - 2830 - 2828 - ... 282- 1
(282 - 1)B = (2832 - 1) + (2830 - 2830) +...+(282 - 282)
(282 - 1)B = (2832 - 1) + 0 + 0 +...+ 0
(282 - 1)B = 2832 - 1
B = (2832 - 1): (282 - 1)
C = \(\dfrac{A}{B}\) = \(\dfrac{28^{32}-1}{28^4-1}\) : \(\dfrac{28^{32}-1}{28^2-1}\)
C = \(\dfrac{28^{32}-1}{28^4-1}\) \(\times\) \(\dfrac{28^2-1}{28^{32}-1}\)
C = \(\dfrac{28^2-1}{28^4-1}\)
C = \(\dfrac{1}{785}\)
Câu d:
\(\dfrac{x-1}{99}\) + \(\dfrac{x-2}{98}\) + \(\dfrac{x-3}{97}\) = \(\dfrac{x-4}{96}\) + \(\dfrac{x-5}{95}\) + \(\dfrac{x-6}{94}\)
(\(\dfrac{x-1}{99}\)-1)+(\(\dfrac{x-2}{98}\)-1)+(\(\dfrac{x-3}{97}\)-1) = (\(\dfrac{x-4}{96}\)-1) + (\(\dfrac{x-5}{95}\)-1)+(\(\dfrac{x-6}{94}\)-1)
\(\dfrac{x-100}{99}\)+\(\dfrac{x-100}{98}\)+\(\dfrac{x-100}{97}\) = \(\dfrac{x-100}{96}\)+\(\dfrac{x-100}{95}\)+\(\dfrac{x-100}{94}\)
\(\dfrac{x-100}{99}\)+\(\dfrac{x-100}{98}\)+\(\dfrac{x-100}{97}\)- \(\dfrac{x-100}{96}\)-\(\dfrac{x-100}{95}\)-\(\dfrac{x-100}{94}\) = 0
(\(x-100\)).(\(\dfrac{1}{99}\)+\(\dfrac{1}{98}\)+\(\dfrac{1}{97}\) - \(\dfrac{1}{96}\)-\(\dfrac{1}{95}\)-\(\dfrac{1}{94}\)) = 0
Vì\(\dfrac{1}{98}< \dfrac{1}{98}< \dfrac{1}{97}< \dfrac{1}{96}< \dfrac{1}{95}< \dfrac{1}{94}\)
Nên (\(\dfrac{1}{99}\) + \(\dfrac{1}{98}\) + \(\dfrac{1}{97}\) )- (\(\dfrac{1}{96}\) + \(\dfrac{1}{95}\) +\(\dfrac{1}{94}\) )< 0
⇒\(x-100\) = 0
Vậy \(x\) = 100

a: Ta có: \(\widehat{xBy}=\widehat{xAz}\)(hai góc đồng vị)
mà hai góc này là hai góc ở vị trí đồng vị
nên By//Az
b: AC là phân giác của góc xAz
=>\(\widehat{xAC}=\widehat{zAC}=\dfrac{\widehat{xAz}}{2}=30^0\)
=>\(\widehat{BAC}=30^0\)
Ta có: \(\widehat{CBA}+\widehat{CBx}=180^0\)(hai góc kề bù)
=>\(\widehat{CBA}+60^0=180^0\)
=>\(\widehat{CBA}=120^0\)
Xét ΔBAC có \(\widehat{BAC}+\widehat{CBA}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+120^0=180^0\)
=>\(\widehat{ACB}=30^0\)
c: BD là phân giác của góc yBA
=>\(\widehat{ABD}=\dfrac{\widehat{yBA}}{2}=60^0\)
Xét ΔBDA có \(\widehat{DBA}+\widehat{DAB}=30^0+60^0=90^0\)
nên ΔBDA vuông tại D
=>AC\(\perp\)BD tại D

Bài 5:
\(A=3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\\ 3A=3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\\ 3A+A=\left(3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\right)+\left(3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\right)\\ 4A=3^{101}+1\\ A=\dfrac{3^{101}+1}{4}\)



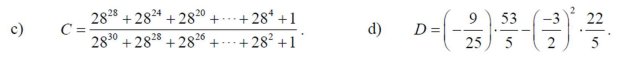
 Giúp mình với các bạn,mình cần gấp câu c1 và câu d2 ạ !
Giúp mình với các bạn,mình cần gấp câu c1 và câu d2 ạ !

a) Để A là phân số thì \(n-2\ne0\Rightarrow n\ne2\)
b) \(A=-3=>\dfrac{2n-7}{n-2}=-3\)
\(=>2n-7=-3\left(n-2\right)\\ =>2n-7=-3n+6\\ =>2n+3n=6+7\\ =>5n=13\\ =>n=\dfrac{13}{5}\left(ktm\right)\)
c) \(A=\dfrac{2n-7}{n-2}=\dfrac{2n-4-3}{n-2}=\dfrac{2\left(n-2\right)-3}{n-2}=2-\dfrac{3}{n-2}\)
Để A nguyên thì: 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ={1; -1; 3; -3}
=> n ∈ {3; 1; 5; -1}
d) Để A lớn nhất thì \(\dfrac{3}{n-2}\) nhỏ nhất
=> \(\dfrac{3}{n-2}=-1\)
=> 3 = -(n - 2)
=> 3 = -n + 2
=> n = -1
e) Để A nhỏ nhất thì \(\dfrac{3}{n-2}\) lớn nhất
=> \(\dfrac{3}{n-2}=1\)
=> 3 = n - 2
=> n = 3 + 2
=> n = 5
f) Để A là phân số tối giản => ƯCLN(2n - 7; n - 2) = 1
=> ƯCLN(3; n - 2) = 1
=> n - 2 không chia hết cho 3
=> n - 2 ≠ 3k
=> n ≠ 3k + 2
g) Gọi d là ước nguyên tố của 2n - 7 và n - 2 ta có:
2n - 7 ⋮ d và n - 2 ⋮ d
=> 2n - 7 ⋮ d và 2(n - 2) ⋮ d
=> (2n - 4) - (2n - 7) ⋮ d
=> 3 ⋮ d
=> d ∈ {1; -1; 3; -3}
Mà d là STN => d = 3
Với d = 3 => 2n - 7 ⋮ 3 => 2(2n - 7) ⋮ 3 => 4n - 7 ⋮ 3
=> 3n + n - 7 ⋮ 3
=> n - 7 ⋮ 3
=> n - 7 = 3k
=> n = 3k + 7
bạn cho mình hỏi sao câu d và câu e lại là -1 và 1 thế ạ?