Gọi số học sinh bốn khối 6,7,8,9 lần lượt là $a$; $b$; $c$; $d$, với $a$; $b$; $c$; $d \in \mathbb{N}^*$ .

Số học sinh khối 6 nhiều hơn khối 9 là $30$ học sinh thì $a - d = 30$.

Số học sinh bốn khối 6,7,8,9 tỉ lệ với $9$; $8$; $7$; $6$ nên:

$a : b: c : d = 9:8:7:6$ hay $\dfrac a9 = \dfrac b8 = \dfrac c7 = \dfrac d6 = \dfrac{a-d}{9-6} = \dfrac{30}3 = 10$.

Từ đó, em suy ra số học sinh mỗi khối. Ví dụ số học sinh khối 6 là: $a = 10.9 = 90$ (học sinh).

olm tới rồi em :

gọi số bi của  Minh, Hùng ,Dũng lần lượt là x,y,z

theo bài ra  ta có : 

\(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}\) => \(\dfrac{3y}{12}=\dfrac{2x}{4}=\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}\) 

=>  \(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3y-2x}{12-4}=\dfrac{40}{8}=5\)

x = 5 x 2 = 10

y = 4 x 5 = 20

z = 5x5 = 25

kết luận:...

nửa chu vi : 32 : 2 = 16 (m)

gọi chiều dài là x, chiều rộng là y theo bài ra ta có :

\(\dfrac{x}{5}\) = \(\dfrac{y}{3}\) 

áp dụng tc dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{x+y}{5+3}=\dfrac{16}{8}=2\)

x = 5.2 = 10

y = 3.2 = 6

chiều dài là 10m

chiều rộng là 6m 

bai 12 dat tinh ri tinh 234+546-765/6

Tổng này không thể tính giá trị cụ thể được banh nhé.

\(\dfrac{a}{c}=\dfrac{a+b}{c+d}=\dfrac{a+b-a}{c+d-c}=\dfrac{b}{d}\) (T/c dãy tỷ số bằng nhau)

\(\Rightarrow\dfrac{a}{b}=\dfrac{c}{d}\) (đpcm)

ab=cdab=cd

⇒ba=dc⇒ba=dc

⇒ba−1=dc−1⇒ba−1=dc−1

⇒b−aa=d−cc⇒−(b−aa)=−(d−cc)⇒b−aa=d−cc⇒−(b−aa)=−(d−cc)

⇒a−ba=c−dc(đpcm)

A B M C D I H

a/

Xét tg CMA và tg BMD có

M là trung điểm BC => MC=MB

MA=MD (gt)

\(\widehat{AMC}=\widehat{BMD}\) (góc đối đỉnh)

=> tg CMA = tg BMD (c.g.c) (đpcm)

=> AC=BD (đpcm)

b/

Ta có

tg CMA = tg BMD (cmt) \(\Rightarrow\widehat{MAC}=\widehat{MDB}\) 

Mà hai gó trên ở vị trí so le trong => AC//BD (đpcm)

c/ Nối M với I và M với H

Xét tg AMH và tg DMI có

AH=DI (gt)

\(\widehat{MAC}=\widehat{MDB}\) (cmt)

tg CMA = tg BMD (cmt) => MA=MD

=> tg AMH = tg DMI (c.g.c) (đpcm)

Ta có

\(\widehat{DMI}+\widehat{AMI}=\widehat{AMD}=180^o\)

Mà tg AMH = tg DMI (cmt) \(\Rightarrow\widehat{DMI}=\widehat{AMH}\)

\(\Rightarrow\widehat{AMH}+\widehat{AMI}=\widehat{IMH}=180^o\)

=> I; H; M thẳng hàng (đpcm)

Gọi số học sinh giỏi ; khá ; trung bình lần lượt là a;b;c

theo bài ra ta có :

a/2=b/3=c/5

a/2+b/3+c/5=a+b+c/2+3+5

                   = 180/10=18

       a/2=18 suy ra a=18.2=36

        b/3=18 suy ra b=18.3=54

         c/5=18 suy ra c=18.5=90

Vậy ....

Mình ko nhớ cách trình bày bạn ạ

Lời giải:
Gọi số hsg, hsk, hstb lần lượt là $a,b,c$. Theo bài ra ta có:

$\frac{a}{2}=\frac{b}{3}=\frac{c}{5}$

$a+b+c=180$

Áp dụng tính chất dãy tỉ số bằng nhau:

$\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{180}{10}=18$

$\Rightarrow a=18.2=36; b=18.3=54; c=18.5=90$ (học sinh)

Từ sau bạn viết đề cẩn thận hơn nhé.

x A y B C M

a) Do AB = AC nên tam giác ABC là tam giác cân, do đó \(\widehat{ABC}=\widehat{ACB}\) (đpcm)

b) Xét hai tam giác AMB và AMC có:

AB = AC (giả thiết)

MB = MC (giả thiết)

AM chung

Suy ra \(\Delta AMB=\Delta AMC\) (c.c.c) (đpcm)

Mình gợi ý nhé

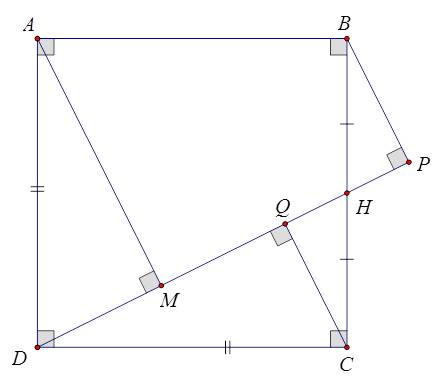
a) Hai tam giác vuông này có hai góc QHC và BHP bằng nhau (đối đỉnh); hai góc HQC và HPB bằng nhau (90^o) nên suy ra hai góc QCH và HBP cũng bằng nhau.

Từ đây chứng minh được \(\Delta QHC=\Delta PHB\left(g.c.g\right)\)

b) \(\widehat{DAM}=90^\circ-\widehat{ADM}=\widehat{QDC}=90^\circ-\widehat{QCD}=\widehat{QCH}\)

c) Từ câu b) suy ra \(\Delta DAM=\Delta CDQ\) (g.c.g) nên DM = CQ.