Em đang thi giúp e với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(2-x\right)^{24}=\left(x-2\right)^{24}=\sum\limits^{24}_{k=0}C^k_{24}.x^k.\left(-2\right)^{24-k}\)
b) Hệ số tổng quát là \(a_k=C^k_{24}\left(-2\right)^{24-k}\) \(\Rightarrow a_9=C^9_{24}.\left(-2\right)^{24-9}=-2^{15}.C^9_{24}\) -> Sai
c) SHTQ: \(T_k=C^k_{24}.x^k.\left(-2\right)^{24-k}\)
\(x^{20}\Rightarrow k=20\) \(\Rightarrow T_4=C^{20}_{24}.x^{20}\left(-2\right)^{24-20}=170016x^{20}\) -> Sai
SHTQ trong khai triển \(\left(2-x\right)^{24}\) là: \(C_{24}^k.\left(-x\right)^k.2^{24-k}=C_{24}^k.\left(-1\right)^k.2^{24-k}.x^k\)
b.
Số hạng chứa \(x^9\Rightarrow k=9\)
\(\Rightarrow a_9=C_{24}^9.\left(-1\right)^9.2^{24-9}=-C_{24}^9.2^{15}\)
c.
Số hạng chứa \(x^{20}\Rightarrow k=20\)
Số hạng đó là:
\(C_{24}^{20}.\left(-1\right)^{20}.2^{24-20}.x^{20}=C_{24}^{20}.2^4.x^{20}=170016.x^{20}\)


Chọn 4 chữ số còn lại: có \(C_6^4\) cách
Chọn 4 chữ số còn lại sao cho có mặt chữ số 0: có \(C_5^3\) cách
Hoán vị 6 chữ số: \(6!\) cách
Hoán vị 6 chữ số sao cho chữ số 0 đứng đầu: \(5!\) cách
\(\Rightarrow C_6^4.6!-C_5^3.5!\) số thỏa mãn

Đường tròn (C) tâm \(I\left(-1;1\right)\) bán kính \(R=\sqrt{17}\)
\(y=-2x+2017\Leftrightarrow2x+y-2017=0\)
Tiếp tuyến vuông góc d nên nhận \(\left(1;-2\right)\) là 1 vtpt
Gọi tiếp tuyến là d' thì pt d' có dạng: \(x-2y+c=0\)
Do d' là tiếp tuyến của (C) nên: \(d\left(I;d'\right)=R\)
\(\Leftrightarrow\dfrac{\left|-1-2.1+c\right|}{\sqrt{1^2+\left(-2\right)^2}}=\sqrt{17}\)
\(\Leftrightarrow\left|c-3\right|=\sqrt{85}\Rightarrow c=3\pm\sqrt{85}\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}x-2y+3+\sqrt{85}=0\\x-2y+3-\sqrt{85}=0\end{matrix}\right.\)

a: Số cách chọn 6 viên bi đỏ là \(C^6_{12}\left(cách\right)\)
Số cách chọn 6 viên bi vàng là \(C^6_8\left(cách\right)\)
=>Tổng số cách chọn 6 viên bi mà chỉ có 1 màu là \(C^6_{12}+C^6_8=952\left(cách\right)\)
Số cách chọn 6 viên bi bất kì là \(C^6_{20}=38760\left(cách\right)\)
Xác suất là \(\dfrac{952}{38760}=\dfrac{7}{285}\)
b: TH1: 5 đỏ, 1 vàng
=>Số cách chọn là \(C^5_{12}\cdot C^1_8=6336\left(cách\right)\)
TH2: 6 đỏ
=>Số cách chọn là \(C^6_{12}=924\left(cách\right)\)
Xác suất để chọn 6 viên bi, trong đó số viên bi đỏ nhiều hơn 4 là \(\dfrac{6336+924}{C^6_{20}}=\dfrac{121}{646}\)
=>Xác suất để chọn 6 viên bi, trong đó số viên bi đỏ ít hơn hoặc bằng 4 là \(1-\dfrac{121}{646}=\dfrac{525}{646}\)
c: Số cách chọn 6 viên bi mà trong đó không có viên màu vàng nào là \(C^6_{12}\left(cách\right)\)
=>Số cách chọn 6 viên bi mà trong đó có ít nhất 1 viên màu vàng là \(C^6_{20}-C^6_{12}=37836\left(cách\right)\)
=>Xác suất là \(\dfrac{37836}{C^6_{20}}=\dfrac{3153}{3230}\)
d: Số cách chọn 6 viên bi sao cho không có đủ 2 màu là \(C^6_8+C^6_{12}=952\left(cách\right)\)
=>Số cách chọn 6 viên bi sao cho có đủ 2 màu là \(C^6_{20}-952=37808\left(cách\right)\)
=>Xác suất là \(\dfrac{37808}{C^6_{20}}=\dfrac{278}{285}\)

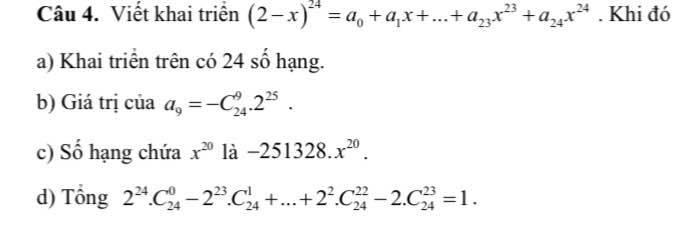
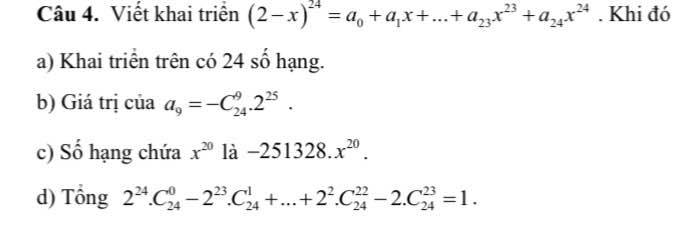

Thi không giúp được bạn nhé!
Mà có giúp cũng đâu có bài đâu mà giúp ^^
Giúp gì thế em nhỉ?