Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(g)\dfrac{x}{xy+y^2}-\dfrac{y}{x^2+xy}\\ =\dfrac{x}{y\left(x+y\right)}-\dfrac{y}{x\left(x+y\right)}\\ =\dfrac{x^2}{xy\left(x+y\right)}-\dfrac{y^2}{xy\left(x+y\right)}\\ =\dfrac{x^2-y^2}{xy\left(x+y\right)}\\ =\dfrac{\left(x+y\right)\left(x-y\right)}{xy\left(x+y\right)}\\ =\dfrac{x-y}{xy}\)
h)
\(\dfrac{x^2+4}{x^2-4}-\dfrac{x}{x+2}-\dfrac{x}{2-x}\\ =\dfrac{x^2+4}{\left(x+2\right)\left(x-2\right)}-\dfrac{x}{x+2}+\dfrac{x}{x-2}\\ =\dfrac{x^2+4}{\left(x+2\right)\left(x-2\right)}-\dfrac{x\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}\\ =\dfrac{x^2+4-x^2+2x+x^2+2x}{\left(x+2\right)\left(x-2\right)}\\ =\dfrac{x^2+4x+4}{\left(x+2\right)\left(x-2\right)}\\ =\dfrac{\left(x+2\right)^2}{\left(x+2\right)\left(x-2\right)}\\ =\dfrac{x+2}{x-2}\)
i)
\(\dfrac{5}{6x-6}+\dfrac{9}{14x-14}+\dfrac{6}{7x-7}\\ =\dfrac{5}{6\left(x-1\right)}+\dfrac{9}{14\left(x-1\right)}+\dfrac{6}{7\left(x-1\right)}\\ =\dfrac{7\cdot5}{42\left(x-1\right)}+\dfrac{3\cdot9}{42\left(x-1\right)}+\dfrac{6\cdot6}{42\left(x-1\right)}\\ =\dfrac{35+27+36}{42\left(x-1\right)}\\ =\dfrac{98}{42\left(x-1\right)}\\ =\dfrac{7}{3\left(x-1\right)}\)

\(x\left(x+4\right)\left(x+6\right)\left(x+10\right)+128\\ =\left[\left(x+6\right)\left(x+4\right)\right]\left[x\left(x+10\right)\right]+128\\ =\left(x^2+6x+4x+24\right)\left(x^2+10x\right)+128\\ =\left(x^2+10x+24\right)\left(x^2+10x\right)+128\\ =\left(x^2+10x\right)^2+24\left(x^2+10x\right)+128\\ =\left(x^2+10x\right)^2+8\left(x^2+10x\right)+16\left(x^2+10x\right)+128\\ =\left(x^2+10x\right)\left[\left(x^2+10x\right)+8\right]+16\left[\left(x^2+10x\right)+8\right]\\ =\left(x^2+10x+8\right)\left(x^2+10x+16\right)\)

\(\left(-2x^5+x^4-3x^3\right):2x^3\)
\(=-x^2+\dfrac{1}{2}x-\dfrac{3}{2}\)
Mình nghĩ đề như này đúng kh bạn? \(\left(-2x^5+x^4-3x^3\right):\left(2x^3\right)\), còn đề như trên thì thực hiện chia 2 rồi nhân x mũ 3 bạn nhé.
\(\left(-2x^5+x^4-3x^3\right):\left(2x^3\right)\\ =\dfrac{-2x^5}{2x^3}+\dfrac{x^4}{2x^3}-\dfrac{3x^3}{2x^3}\\ =-x^2+\dfrac{x}{2}-\dfrac{3}{2}\)

a: Đề sai rồi bạn
b: Xét ΔIBK và ΔICN có
IB=IC
\(\widehat{BIK}=\widehat{CIN}\)(hai góc đối đỉnh)
IK=IN
Do đó: ΔIBK=ΔICN
=>BK=CN

\(x^2-x-2001\cdot2002\)
\(=x^2-2002x+2001x-2001\cdot2002\)
\(=x\left(x-2002\right)+2001\left(x-2002\right)=\left(x-2002\right)\left(x+2001\right)\)

Lời giải:
Đặt $2x-1=a$
\(a^6=a^8\\ \Leftrightarrow a^8-a^6=0\\ \Leftrightarrow a^6(a^2-1)=0\\ \Leftrightarrow a^6=0\text{ hoặc } a^2-1=0\\ \Leftrightarrow a=0 \text{ hoặc } a=\pm 1\\ \Leftrightarrow 2x-1=0 \text{ hoặc } 2x-1=1 \text{ hoặc } 2x-1=-1\)
$\Leftrightarrow x=\frac{1}{2}$ hoặc $x=1$ hoặc $x=0$

Lời giải:
$f(x)=x^{6n}-x^{3n}+1=x^{3n}(x^{3n}-1)+1$
$=x^{3n}[(x^3)^n-1^n]+1$
$=x^{3n}(x^3-1)[(x^3)^{n-1}+(x^3)^{n-2}+...+1]+1$
$=x^{3n}(x^2+x+1)(x-1)[(x^3)^{n-1}+(x^3)^{n-2}+...+1]+1$
$\Rightarrow f(x)$ chia $x^2+x+1$ dư $1$
$\Rightarrow f(x)$ không chia hết cho $g(x)$

\(\left(x-2\right)^3-\left(x-2\right)\left(x^2+2x+4\right)=0\\ \Leftrightarrow\left(x-2\right)\left[\left(x-2\right)^2-\left(x^2+2x+4\right)\right]=0\\ \Leftrightarrow\left(x-2\right)\left(x^2-4x+4-x^2-2x-4\right)=0\\ \Leftrightarrow\left(x-2\right).\left(-6x\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\-6x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
Cách làm khác:
\(\left(x-2\right)^3-\left(x-2\right)\left(x^2+2x+4\right)=0\\ \Leftrightarrow x^3-3.x^2.2+3.x.2^2-2^3-\left(x^3-2^3\right)=0\\ \Leftrightarrow x^3-6x^2+12x-8-x^3+8=0\\ \Leftrightarrow-6x^2+12x=0\\ \Leftrightarrow-6x\left(x-2\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
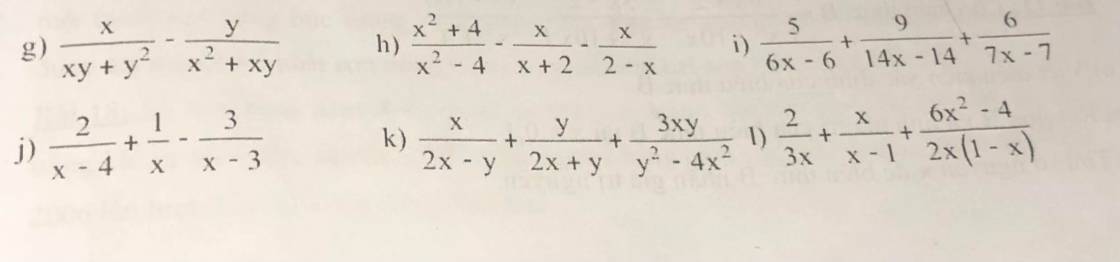
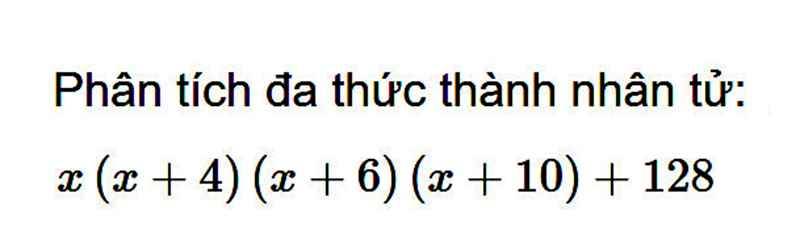
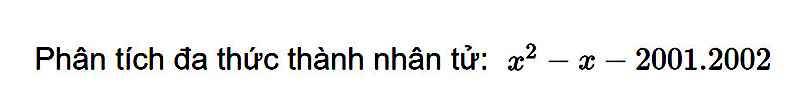
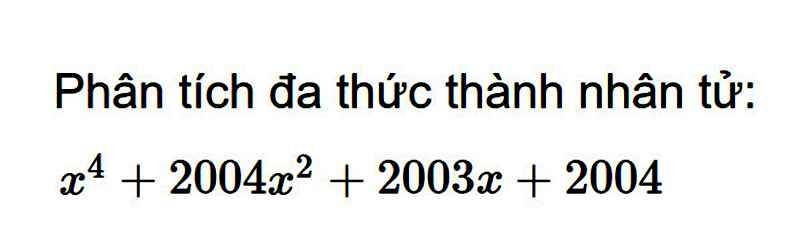

\(x^4+6x^3+7x^2-6x+1\\ =\left(x^4+6x^3+9x^2\right)-2x^2-6x+1\\ =\left[\left(x^2\right)^2+2\cdot x^2\cdot3x+\left(3x\right)^2\right]-2\left(x^2+3x\right)+1\\ =\left(x^2+3x\right)^2-2\left(x^2+3x\right)+1^2\\=\left(x^2+3x-1\right)^2\)