. Cho tam giác ABC. Lấy điểm M trên BC sao cho CM = 2 BM; lấy điểm N trên AC sao cho 3AN = 2CN. Nối M với N, ta được tam giác MNC có diện tích 30 cm2. Tính diện tích tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(2^2=2\cdot2=4\)
\(3^2=3\cdot3=9\)
\(4^2=4\cdot4=16\)
\(5^2=5\cdot5=25\)
\(6^2=6\cdot6=36\)
\(7^2=7\cdot7=49\)
\(8^2=8\cdot8=64\)
\(9^2=9\cdot9=81\)
\(10^2=10\cdot10=100\)
\(11^2=11\cdot11=121\)
\(12^2=12\cdot12=144\)

a: \(\left(\dfrac{1}{4\cdot7}+\dfrac{1}{7\cdot10}+...+\dfrac{1}{73\cdot76}\right)\cdot x^2=2\dfrac{16}{19}\)
=>\(\dfrac{1}{3}\left(\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{73\cdot76}\right)\cdot x^2=2+\dfrac{16}{19}=\dfrac{54}{19}\)
=>\(\dfrac{1}{3}\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{73}-\dfrac{1}{76}\right)\cdot x^2=\dfrac{54}{19}\)
=>\(\dfrac{1}{3}\left(\dfrac{1}{4}-\dfrac{1}{76}\right)\cdot x^2=\dfrac{54}{19}\)
=>\(\dfrac{1}{3}\cdot\dfrac{18}{76}\cdot x^2=\dfrac{54}{19}\)
=>\(\dfrac{6}{76}\cdot x^2=\dfrac{54}{19}\)
=>\(x^2=\dfrac{54}{19}:\dfrac{6}{76}=\dfrac{54}{19}\cdot\dfrac{76}{6}=9\cdot4=36\)
=>\(\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
b: \(2^x+2^{x+2}=\dfrac{200}{19}\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{19\cdot20}\right)\)
=>\(2^x+2^x\cdot4=\dfrac{200}{19}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)\)
=>\(5\cdot2^x=\dfrac{200}{19}\left(1-\dfrac{1}{20}\right)=\dfrac{200}{19}\cdot\dfrac{19}{20}=10\)
=>\(2^x=2\)
=>x=1

\(2015^{2016}-1=\left(2015-1\right)\cdot\left(2015^{2015}+2015^{2014}+...+1\right)\)
\(=2014\cdot\left(2015^{2015}+2015^{2014}+...+1\right)⋮2014\)

Gọi số lập được có dạng là \(\overline{abcd}\)
a có 3 cách chọn
b có 3 cách chọn
c có 2 cách chọn
d có 1 cách chọn
Do đó: Có \(3\cdot3\cdot2\cdot1=18\left(cách\right)\)

\(3^{x+5}-4\cdot3^{12}=5\cdot3^{12}\\ =>3^{x+5}=5\cdot3^{12}+4\cdot3^{12}\\ =>3^{x+5}=3^{12}\cdot\left(4+5\right)\\ =>3^{x+5}=3^{12}\cdot9\\ =>3^{x+5}=3^{12}\cdot3^2\\ =>3^{x+5}=3^{14}\\ =>x+5=14\\ =>x=14-5\\ =>x=9\)

Khoảng cách giữa hai phần tử là: `8-2=6`
Số phần tử của G là:
`(386-2):6+1=65` (số hạng)
Vậy: ...

Sửa đề: F là giao điểm của DA
Xét ΔBAC có
M,E lần lượt là trung điểm của BA,BC
=>ME là đường trung bình của ΔBAC
=>ME//AC và \(ME=\dfrac{AC}{2}\left(1\right)\)
Xét ΔDAC có
F,N lần lượt là trung điểm của DA,DC
=>FN là đường trung bình của ΔDAC
=>FN//AC và \(FN=\dfrac{AC}{2}\left(2\right)\)
Từ (1),(2) suy ra ME//FN và ME=FN
Xét tứ giác MENF có
ME//FN
ME=FN
Do đó: MENF là hình bình hành
=>MN cắt EF tại trung điểm của mỗi đường
=>O là trung điểm của MN
=>\(\dfrac{MO}{ON}=1\)

\(n\left(n+1\right)\left(2n+1\right)\\ =n\left(n+1\right)\left[2n-2+3\right]\\ =n\left(n+1\right)\left(2n-2\right)+3n\left(n+1\right)\\ =2\left(n-1\right)n\left(n+1\right)+3n\left(n+1\right)\)
Ta có:
`+)(n-1)n(n+1)` là tích của 3 số tự nhiên liên tiếp `=>(n-1)n(n+1)` chia hết cho 3
`=>2(n-1)n(n+1)` chia hết cho 6 (1)
`+)n(n+1)` là tích của 2 số tự nhiên liên tiếp `=>n(n+1)` chia hết cho 2
`=>3n(n+1)` chia hết cho 6 (2)
Từ (1) và (2) => `n(n+1)(2n+1)` chia hết cho 6

\(\left[19\left(4\cdot2^3+18\right)-9\cdot50\right]:5^2\\ =\left[19\left(4\cdot8+18\right)-450\right]:25\\ =\left[19\cdot50-450\right]:25\\ =\left[950-450\right]:25\\ =500:25\\ =20\)
\(\left[19\left(4\cdot2^3+18\right)-9\cdot50\right]:5^2\\ =\left[19\left(4\cdot8+18\right)-9\cdot50\right]:25\\ =\left[19\left(32+18\right)-9\cdot50\right]:25\\ =\left(19\cdot50-9\cdot50\right):25\\ =50\cdot\left(19-9\right):25\\ =\left(50:25\right)\cdot10\\ =2\cdot10\\ =20\)
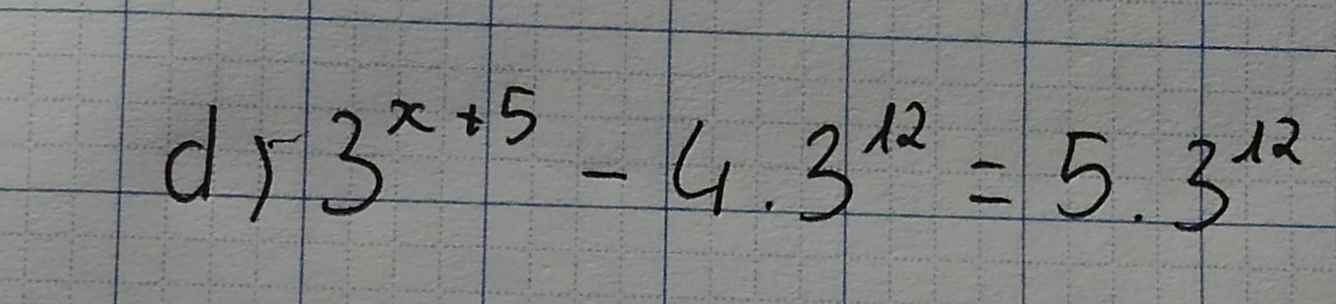
3AN=2CN
=>\(AN=\dfrac{2}{3}CN\)
=>\(AN=\dfrac{2}{5}AC\)
=>\(CN=\dfrac{3}{5}AC\)
CM=2BM
=>\(BM=\dfrac{1}{3}BC;CM=\dfrac{2}{3}BC\)
Vì \(CN=\dfrac{3}{5}AC\)
nên \(S_{MNC}=\dfrac{3}{5}\cdot S_{AMC}\)
=>\(S_{AMC}=30:\dfrac{3}{5}=50\left(cm^2\right)\)
Vì \(CM=\dfrac{2}{3}BC\)
nên BC=1,5CM
=>\(S_{ABC}=1,5\cdot S_{AMC}=1,5\cdot50=75\left(cm^2\right)\)