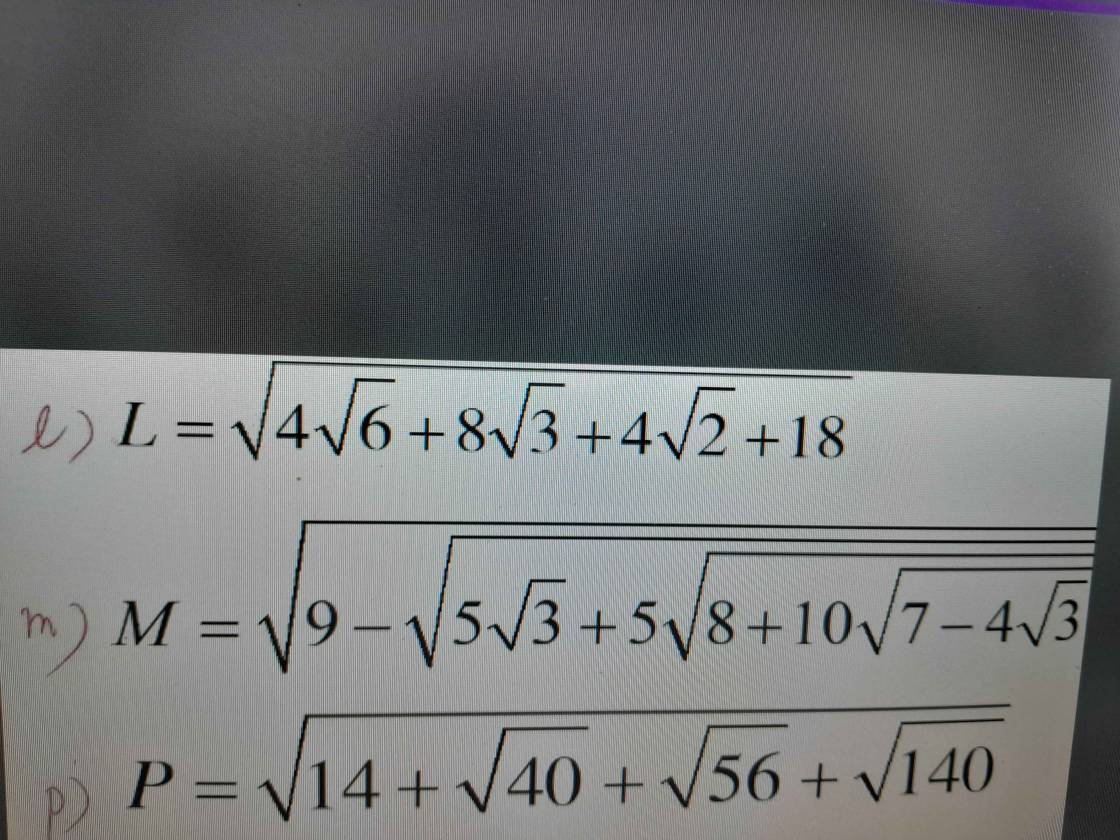Gọi T là giao điểm của 2 tiếp tuyến tại A và B của (O). Qua N kẻ đường thẳng song song với AM cắt AB tại C. Gọi I là giao điểm của AB và MN.

 Khi đó, theo tính chất của 2 tiếp tuyến cắt nhau, ta có \(TA=TB\) \(\Rightarrow\Delta TAB\) cân tại T \(\Rightarrow\widehat{TBA}=\widehat{TAB}\)

 Vì NC//TA nên \(\widehat{NCB}=\widehat{TAB}\) (2 góc đồng vị) 

 Từ đó \(\Rightarrow\widehat{TBA}=\widehat{NCB}\) \(\Rightarrow\Delta NCB\) cân tại N 

 \(\Rightarrow NC=NB\)

 Mà \(NB=MA\) nên \(NC=MA\)

 Do đó tứ giác NAMC là hình bình hành (vì có NC//MA và \(NC=MA\))

 \(\Rightarrow\) MN và AC cắt nhau tại trung điểm I của mỗi đoạn

 \(\Rightarrow\) I là trung điểm MN

 \(\Rightarrow\) AB chia đôi MN (đpcm)

\(\dfrac{2\left(1-3x\right)}{5}-2+\dfrac{3x}{10}=8-\dfrac{2x+1}{4}\)

\(\Leftrightarrow\dfrac{8\left(1-3x\right)}{20}-\dfrac{40}{20}+\dfrac{6x}{20}=\dfrac{160}{20}-\dfrac{5\left(2x+1\right)}{20}\)

\(\Leftrightarrow8\left(1-3x\right)-40+6x=160-5\left(2x+1\right)\)

\(\Leftrightarrow8-24x-40+6x=160-10x-5\)

\(\Leftrightarrow-18x-32=155-10x\)

\(\Leftrightarrow-18x+10x=155+32\)

\(\Leftrightarrow-8x=187\)

\(\Leftrightarrow x=-\dfrac{187}{8}\)

Vậy: ... 

l: \(L=\sqrt{4\sqrt{6}+8\sqrt{3}+4\sqrt{2}+18}\)

\(=\sqrt{12+4+2+2\cdot2\sqrt{3}\cdot2+2\cdot2\sqrt{3}\cdot\sqrt{2}+2\cdot2\cdot\sqrt{2}}\)

\(=\sqrt{\left(2\sqrt{3}+\sqrt{2}+2\right)^2}=2\sqrt{3}+\sqrt{2}+2\)

m: \(M=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{8+10\sqrt{7-4\sqrt{3}}}}}\)

\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{8+10\sqrt{\left(2-\sqrt{3}\right)^2}}}}\)

\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{8+10\left(2-\sqrt{3}\right)}}}\)

\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{8+20-10\sqrt{3}}}}\)

\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)

\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)

\(=\sqrt{9-\sqrt{5\sqrt{3}+5\left(5-\sqrt{3}\right)}}\)

\(=\sqrt{9-\sqrt{5\sqrt{3}+25-5\sqrt{3}}}=\sqrt{9-\sqrt{25}}=\sqrt{4}=2\)

p: \(P=\sqrt{14+\sqrt{40}+\sqrt{56}+\sqrt{140}}\)

\(=\sqrt{14+2\cdot\sqrt{2}\cdot\sqrt{5}+2\cdot\sqrt{2}\cdot\sqrt{7}+2\cdot\sqrt{5}\cdot\sqrt{7}}\)

\(=\sqrt{5+2+7+2\cdot\sqrt{2}\cdot\sqrt{5}+2\cdot\sqrt{2}\cdot\sqrt{7}+2\cdot\sqrt{5}\cdot\sqrt{7}}\)

\(=\sqrt{\left(\sqrt{2}+\sqrt{5}+\sqrt{7}\right)^2}=\sqrt{2}+\sqrt{5}+\sqrt{7}\)

b: \(cos14=sin76;cos37=sin53\)

Vì 47<48<53<76 nên \(sin47< sin48< sin53< sin76\)

=>\(sin47< sin48< cos37< cos14\)

c: \(cot25=tan65;cot38=tan52\)

Vì 52<62<65<73

nên \(tan52< tan62< tan65< tan73\)

=>\(cot38< tan63< cot25< tan73\)

a: Vì 75>45

nên \(tan75>1\)

Vì 40<45

nên \(cot40>1\)

\(cot40=tan50;tan75=tan75\)

mà \(tan50< tan75\)

nên \(1< cot40< tan75\left(1\right)\)

\(cos56=sin34;sin50=sin50\)

mà 34<50

nên \(sin34< sin50< 1\)

=>\(cos56< sin50< 1\left(2\right)\)

Từ (1),(2) suy ra \(cos56< sin50< cot40< tan75\)

Xét ΔABC vuông tại A có \(\widehat{B}+\widehat{C}=90^0\)

nên \(sinB=cosC=\dfrac{4}{5}\)

\(sin^2B+cos^2B=1\)

=>\(cos^2B=1-\left(\dfrac{4}{5}\right)^2=\dfrac{9}{25}=\left(\dfrac{3}{5}\right)^2\)

=>\(cosB=\dfrac{3}{5}\)

\(tanB=\dfrac{sinB}{cosB}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)

\(cotB=\dfrac{1}{tanB}=\dfrac{3}{4}\)

Vì tam giác ABC vuông tại A

Nên: \(\widehat{B}+\widehat{C}=90^o\\ \Rightarrow0^o< \widehat{C}< 90^o\)

\(\Rightarrow0< \sin C< 1\) 

Ta có: \(\sin^2C+\cos^2C=1\Rightarrow\sin^2C=1-\left(\dfrac{4}{5}\right)^2=\dfrac{9}{25}\\ \Rightarrow\sin C=\dfrac{3}{5}\)

Lại có: \(\tan C=\dfrac{\sin C}{\cos C}=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\dfrac{3}{4}\\ \cot C=\dfrac{1}{\tan C}=\dfrac{4}{3}\)

\(5x^2-2x+1=\left(4x-1\right)\sqrt{x^2}+1\)

\(\Rightarrow5x^2-2x=\left(4x-1\right)x\)

\(\Rightarrow5x^2-2x=4x^2-x\)

\(\Rightarrow5x^2-4x^2-2x+x=0\)

\(\Rightarrow x^2-x=0\)

\(\Rightarrow x\left(x-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x-1=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

Vậy x=0 hoặc x=1

\(\left[{}\begin{matrix}2x+3=x-5\\2x+3=5-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\3x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=\dfrac{2}{3}\end{matrix}\right.\)

14: Gọi số bộ linh kiện trong 1 ngày tổ B lắp được là x(bộ)

(Điều kiện: \(x\in Z^+\))

Số bộ linh kiện trong 1 ngày tổ A lắp được là x+20(bộ)

Trong 5 ngày, tổ A lắp được 5(x+20)(bộ)

Trong 4 ngày, tổ B lắp được 4x(bộ)

Theo đề, ta có phương trình:

5(x+20)+4x=1900

=>9x=1800

=>x=200(nhận)

vậy: số bộ linh kiện trong 1 ngày tổ B lắp được là 200(bộ)

số bộ linh kiện trong 1 ngày tổ A lắp được là 200+20=220(bộ)

Bài 11:

Gọi số trận thắng của Arsenal mùa đó là x(trận)

(Điều kiện: \(x\in Z^+\))

Số trận hòa mùa đó là 38-x(trận)

Số điểm nhận được cho các trận thắng là 3x(điểm)

Số điểm nhận được cho các trận hòa là 1(38-x)=38-x(điểm)

Tổng số điểm là 90 điểm nên ta có:

3x+38-x=90

=>2x=90-38=52

=>x=26(nhận)

Vậy: Số trận thắng mùa đó của Arsenal là 26 trận

Bạn nên ghi hẳn đề ra để mọi người hỗ trợ nhanh hơn nhé.