Tìm giá trị nhỏ nhất của biểu thức M = |x – 22| + |x + 12|
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
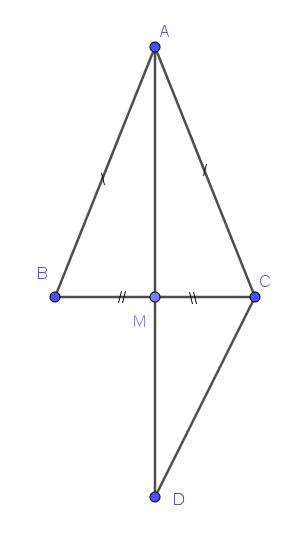
a. Xét tam giác $AMB$ à $AMC$ có:
$AB=AC$ (do tam giác $ABC$ cân tại $A$)
$MB=MC$ (do $M$ là trung điểm $BC$
$AM$ chung
$\Rightarrow \triangle AMB=\triangle AMC$ (c.c.c)
b.
Từ tam giác bằng nhau phần a
$\Rightarrow \widehat{BAM}=\widehat{CAM}$
$\Rightarrow AM$ là phân giác $\widehat{BAC}$
c.
Xét tam giác $ABM$ và $DCM$ có:
$BM=CM$
$AM=DM$ (gt)
$\widehat{AMB}=\widehat{DMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle DCM$ (c.g.c)
$\Rightarrow \widehat{BAM}=\widehat{CDM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CD$

a) \(1,2-3^2+7,5:3\)
\(=1,2-9+2,5\)
\(=-7,8+2,5=-5,3\)
b) \(\dfrac{9^{11}\cdot25^6}{15^6\cdot27^5}=\dfrac{\left(3^2\right)^{11}\cdot\left(5^2\right)^6}{\left(3\cdot5\right)^6\cdot\left(3^3\right)^5}=\dfrac{3^{22}\cdot5^{12}}{3^6\cdot5^6\cdot3^{15}}\)
\(=\dfrac{3^{22}\cdot5^{12}}{3^{21}\cdot5^6}=3\cdot5^6=46875\)
c) \(\left|\dfrac{3}{8}-\dfrac{9}{16}\right|-\sqrt{\dfrac{25}{64}}+\left(\dfrac{7}{16}\right)^5:\left(\dfrac{7}{16}\right)^4\)
\(=\left|\dfrac{6}{16}-\dfrac{9}{16}\right|-\sqrt{\dfrac{5^2}{8^2}}+\dfrac{7}{16}\)
\(=\left|-\dfrac{3}{16}\right|-\sqrt{\left(\dfrac{5}{8}\right)^2}+\dfrac{7}{16}\)
\(=\dfrac{3}{16}-\dfrac{5}{8}+\dfrac{7}{16}\)
\(=\dfrac{3}{16}-\dfrac{10}{16}+\dfrac{7}{16}\)
\(=\dfrac{3-10+7}{16}=0\)
d) \(\sqrt{\left(\dfrac{-1}{4}\right)^2}-3.\sqrt{\dfrac{25}{81}}+\left|\dfrac{7}{4}-\dfrac{1}{3}\right|\)
\(=\left|\dfrac{-1}{4}\right|-3.\sqrt{\left(\dfrac{5}{9}\right)^2}+\left|\dfrac{17}{12}\right|\\ =\dfrac{1}{4}-3.\left|\dfrac{5}{9}\right|+\dfrac{17}{12}\\ =\dfrac{1}{4}-3.\dfrac{5}{9}+\dfrac{17}{12}\\ =\dfrac{1}{4}-\dfrac{15}{9}+\dfrac{17}{12}\\ =-\dfrac{17}{12}+\dfrac{17}{12}=0\)

\(A=\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\)
\(3A=1+\dfrac{2}{3}+\dfrac{3}{3^2}+...+\dfrac{100}{3^{99}}\)
\(\Rightarrow3A-A=1+\dfrac{2}{3}-\dfrac{1}{3}+\dfrac{3}{3^2}-\dfrac{2}{3^2}+\dfrac{4}{3^3}-\dfrac{3}{3^3}+...+\dfrac{100}{3^{99}}-\dfrac{99}{3^{99}}-\dfrac{100}{3^{100}}\)
\(\Rightarrow2A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)
\(\Rightarrow6A=3+1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\)
\(\Rightarrow6A-2A=3-\dfrac{101}{3^{99}}+\dfrac{100}{3^{100}}\)
\(\Rightarrow4A=3-\dfrac{203}{3^{100}}< 3\)
\(\Rightarrow A< \dfrac{3}{4}\)

Giá bán của một chiếc iphone ban đầu là:
25 000 000 x 160 : 100 = 40 000 000 (đồng)
Số tiền lần đầu thu được khi bán 90 chiếc iphone là
40 000 000 x 90 = 3 600 000 000 (đồng)
Số iphone còn lại sau đợt bán thứ nhất là:
120 - 90 = 30 (chiếc)
Giá của mỗi chiếc iphone còn lại là:
40 000 000 x (100% - 50%) = 20 000 000 (đồng)
Số tiền thu được khi bán 30 chiếc iphone còn lại là:
20 000 000 x 30 = 600 000 000 (đồng)
Tổng số tiền điện máy xanh thu được khi bán hết 120 chiếc iphone là:
3 600 000 000 + 600 000 000 = 4 200 000 000 (đồng)
Giá vốn của 120 chiếc iphone là:
25 000 000 x 120 = 3 000 000 000 (đồng)
Sau khi bán hết 120 chiếc iphone điện máy xanh lãi và lãi số tiền là:
4 200 000 000 - 3 000 000 000 = 1 200 000 000 (đồng)
Đáp số:...
Giá bán của một chiếc iphone ban đầu là:
25 000 000 x 160 : 100 = 40 000 000 (đồng)
Số tiền lần đầu thu được khi bán 90 chiếc iphone là
40 000 000 x 90 = 3 600 000 000 (đồng)
Số iphone còn lại sau đợt bán thứ nhất là:
120 - 90 = 30 (chiếc)
Giá của mỗi chiếc iphone còn lại là:
40 000 000 x (100% - 50%) = 20 000 000 (đồng)
Số tiền thu được khi bán 30 chiếc iphone còn lại là:
20 000 000 x 30 = 600 000 000 (đồng)
Tổng số tiền điện máy xanh thu được khi bán hết 120 chiếc iphone là:
3 600 000 000 + 600 000 000 = 4 200 000 000 (đồng)
Giá vốn của 120 chiếc iphone là:
25 000 000 x 120 = 3 000 000 000 (đồng)
Sau khi bán hết 120 chiếc iphone điện máy xanh lãi và lãi số tiền là:
4 200 000 000 - 3 000 000 000 = 1 200 000 000 (đồng)
Đáp số:...

A = \(\dfrac{1}{2}\) + \(\dfrac{1}{3}\) + \(\dfrac{1}{4}\) +...+ \(\dfrac{1}{2007}\) + \(\dfrac{1}{2008}\) + \(\dfrac{1}{2009}\)
B = 2008 + \(\dfrac{2007}{2}\) + \(\dfrac{2006}{3}\)+ ... + \(\dfrac{2}{2007}\) + \(\dfrac{1}{2008}\)
B = (1 + \(\dfrac{2007}{2}\)) + (1 + \(\dfrac{2006}{3}\)) + .. + (1 + \(\dfrac{2}{2007}\)) + (1 + \(\dfrac{1}{2008}\)) + 1
B = \(\dfrac{2+2007}{2}\) + \(\dfrac{3+2006}{3}\) +... + \(\dfrac{2007+2}{2007}\) + \(\dfrac{2008+1}{2008}\) + \(\dfrac{2009}{2009}\)
B = \(\dfrac{2009}{2}\) + \(\dfrac{2009}{3}\) + ... + \(\dfrac{2009}{2007}\) + \(\dfrac{2009}{2008}\) + \(\dfrac{2009}{2009}\)
B = 2009.( \(\dfrac{1}{2}\) + \(\dfrac{1}{3}\) + ....+ \(\dfrac{1}{2007}\) + \(\dfrac{1}{2008}\) + \(\dfrac{1}{2009}\))
Tỉ số của \(\dfrac{A}{B}\)
\(\dfrac{A}{B}\)= \(\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2007}+\dfrac{1}{2008}+\dfrac{1}{2009}}{2009.\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2007}+\dfrac{1}{2008}+\dfrac{1}{2009}\right)}\)
\(\dfrac{A}{B}\) = \(\dfrac{1}{2009}\)

\(x^2=3+5+2\sqrt{15}=8+\sqrt{60}\)
\(y^2=2+6+2\sqrt{12}=8+\sqrt{48}\)
Mà \(60>48\Rightarrow\sqrt{60}>\sqrt{48}\Rightarrow8+\sqrt{10}>8+\sqrt{48}\)
\(\Rightarrow x^2>y^2\Rightarrow x>y\) (do x;y đều dương)

(2y-1)¹⁰=(2y-1)²⁰
→ (2y-1)²⁰-(2y-1)¹⁰=0
→ (2y-1)¹⁰.[(2y-1)¹⁰-1]=0
→ (2y-1)¹⁰=0 hay (2y-1)¹⁰-1=0
→ 2y-1=0 hay 2y-1=1 hay 2y-1=-1
→ y=½ hay y=1 hay y=0

Lãi suất:
214 400 000 : 200 000 000 x 100% - 100% = 7,2%
Đáp số:.......
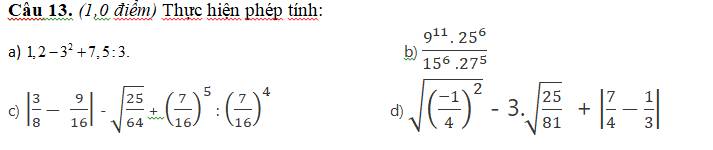
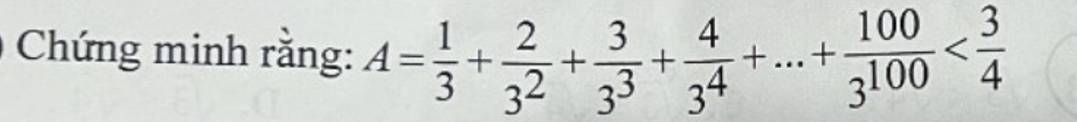

???
\(M=\left|x-22\right|+\left|x+12\right|\)
\(M=\left|22-x\right|+\left|x+12\right|\ge\left|22-x+x+12\right|\)
\(M=\left|22-x\right|+\left|x+12\right|\ge34\)
\(M\ge34\)
Dấu "\(=\)" xảy ra khi:
\(\left(22-x\right)\left(x+12\right)\ge0\)
\(TH1:22-x\ge0;x+12\ge0\)
\(\Rightarrow22\ge x\ge-12\)
\(TH2:22-x\le0;x+12\ge0\)
\(\Rightarrow22\le x;x\ge12\left(vô.lý\right)\)
Vậy \(GTNN\) của \(M\) là \(34\) khi \(22\ge x\ge-12\)