Tìm 2 số biết tổng của chúng bằng 186 và biết số lớn chia cho số bé bằng 2 dư 12.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(-x+5=3x+\left(-11\right)\)
\(-x-3x=-5+\left(-11\right)\)
\(-4x=-16\)
\(x=\left(-16\right):\left(-4\right)\)
\(x=4\)
Đa dạng cách nhé :Đ
`-x + 5 = 3x + (-11)`
`=> 3x + x = 5 + 11`
`=> 4x = 16`
`=> x = 16 : 4`
`=> x = 4`

`overline{mn24p03ks}= overline{m00000000} +overline{n0000000}+ 2000000+ 400000+ overline{p0000} +300+ overline{k0}+ s`
=> Chọn C

Gọi chiều dài màn hình là `x` (cm)
ĐK: `x>0`
Đổi: 17inch ≃ 43,18 (cm)
Chiều cao màn hình là: `5/8x(cm)`
Áp dụng định lý Pythagore ta có:
\(x^2+\left(\dfrac{5}{8}x\right)^2=43,18^2\\ < =>x^2+\dfrac{25}{64}x^2=1864,5124\\ < =>\dfrac{79}{64}x^2=1864,5124\\ < =>x^2\approx1510,4\\ < =>x\approx38,9\left(cm\right)\left(x>0\right)\)
=> Chiều cao của màn hình là: `5/8*38,9≃24,3(cm)`
Vậy:
Gọi x (cm) là chiều rộng màn hình (x > 0)
Chiều dài màn hình là:
 Đổi 17 inch ≈ 43,2 cm
Đổi 17 inch ≈ 43,2 cm
 Theo đề bài, ta có phương trình:
Theo đề bài, ta có phương trình:
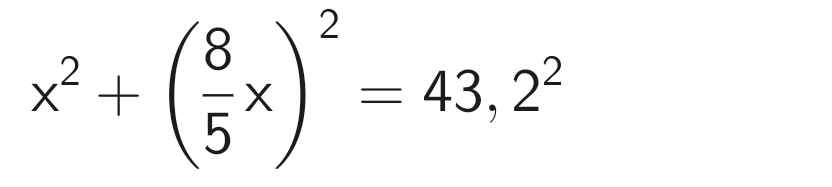
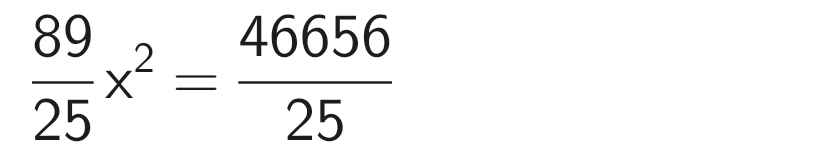
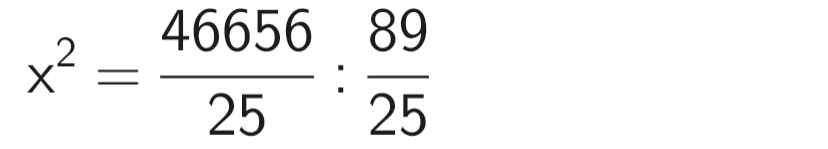

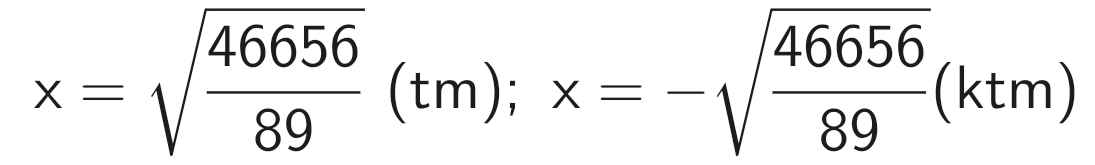
⇒ x ≈ 22,9 (cm)
Vậy chiều rộng màn hình là 22,9 cm, chiều dài màn hình là 22,9.1,6 ≈ 36,6 cm

a.
\(\left\{{}\begin{matrix}S=x_1+x_2=7\\P=x_1x_2=10\end{matrix}\right.\)
Theo định lý Viet đảo, \(x_1;x_2\) là nghiệm:
\(x^2-7x+10=0\)
Trình bày tương tự câu a ta có:
b.
\(x^2-2x-35=0\)
c.
\(x^2+13x+36=0\)

Giá sau khi giảm so với giá bìa:
1 - 40% = 60%
Giá bìa quyển sách là:
69600 : 60% = 116000 (đồng)

`2/5 + 3/4 :x= -1/2 `
`=> 3/4 :x = -1/2 - 2/5`
`=> 3/4 : x = -9/10`
`=> x = 3/4 : (-9/10)`
`=> x = 3/4 . (-10/9) `
`=> x = -5/6`
Vậy `x = -5/6`
------------------
`5/7 - 2/3 x = 4/5`
`=> 2/3 x = 5/7 - 4/5`
`=> 2/3 x = -3/35`
`=> x = -3/35 : 2/3`
`=> x = -3/35 . 3/2`
`=> x = -9/70`
Vậy `x = -9/70`
------------------
`1/2 x + 3/5 x = -2/3`
`=> (1/2 + 3/5) x = -2/3`
`=> 11/10 x = -2/3`
`=> x = -2/3 : 11/10`
`=> x = -2/3 . 10/11`
`=> x = -20/33`
Vậy ` x = -20/33`
------------------
`4/7 x - x = -9/14`
`=> (4/7 - 1) x = -9/14`
`=> -3/7 x = -9/14`
`=> 3/7 x = 9/14`
`=> x = 9/14 : 3/7`
`=> x = 9/14 . 7/3`
`=> x = 3/2`
Vậy `x = 3/2`

\(-x^3+3x-7+2m=0\)
\(\Leftrightarrow x^3-3x+7=2m\)
Xét hàm: \(f\left(x\right)=x^3-3x+7\)
\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
Bảng biến thiên:
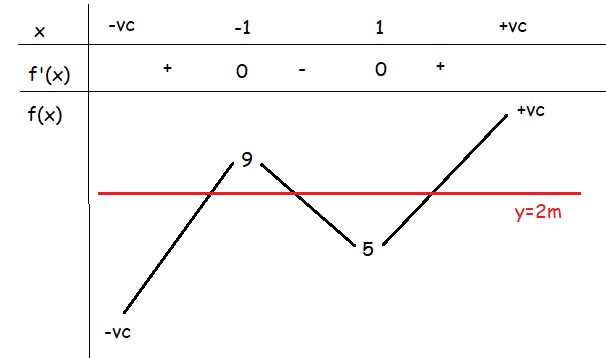
Từ BBT ta thấy pt có 3 nghiệm pb hay \(y=2m\) cắt \(y=f\left(x\right)\) tại 3 điểm pb
\(\Leftrightarrow5< 2m< 9\Rightarrow\dfrac{5}{2}< m< \dfrac{9}{2}\)

\(\left(2x-\dfrac{1}{3}\right)^2=-\dfrac{8}{15}\times\dfrac{15}{27}:\left(2x-\dfrac{1}{3}\right)\)
\(\left(2x-\dfrac{1}{3}\right)^2\times\left(2x-\dfrac{1}{3}\right)=-\dfrac{8}{27}\)
\(\left(2x-\dfrac{1}{3}\right)^3=\left(-\dfrac{2}{3}\right)^3\)
\(2x-\dfrac{1}{3}=-\dfrac{2}{3}\)
\(2x=\dfrac{1}{3}-\dfrac{2}{3}\)
\(2x=-\dfrac{1}{3}\)
\(x=-\dfrac{1}{6}\)

Áp dụng t/c dãy tỉ số bằng nhau: \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\)
Từ \(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\Rightarrow\dfrac{\left(a+b\right)^3}{\left(c+d\right)^3}=\dfrac{a^3}{c^3}=\dfrac{b^3}{d^3}=\dfrac{a^3+b^3}{c^3+d^3}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có: \(VT=\dfrac{a^3+b^3}{c^3+d^3}=\dfrac{bk^3+b^3}{dk^3+d^3}=\dfrac{b.\left(k+1\right)^3}{d.\left(k+1\right)^3}=\dfrac{b}{d}\)
\(VP=\dfrac{\left(a+b\right)^3}{\left(c+d\right)^3}=\dfrac{\left(bk+b\right)^3}{\left(dk+d\right)^3}=\dfrac{b.\left(k+1\right)^3}{d.\left(k+1\right)^3}=\dfrac{b}{d}\)
Vậy \(VT=VP\left(đpcm\right)\)
____________
VT = vế trái
VP = vế phải
\(#NqHahh\)
Do số lớn chia cho số bé bằng 2 dư 12 nên số lớn gấp số bé 2 lần và thêm 12 đơn vị
Gọi `a =` Số lớn `- 12`
Ta có sơ đồ:
`a`: `2` phần
Số bé: `1 ` phần
Tổng của số `a` và Số bé là:
`186 - 12 = 174 `
Tổng số phần bằng nhau là:
`2+1 = 3` (phần)
Giá trị 1 phần là:
`174 : 3 = 58 `
Số bé là:
`58 xx 1 = 58`
Số lớn là:
`58 xx 2 + 12 = 128`
Đáp số: ...
Đây là dạng toán nâng cao phép chia có dư, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay. Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Coi số bé là một phần ta có sơ đồ
Theo sơ đồ ta có
Số bé là: (186 - 12) : (2 + 1) = 58
Số lớn là: 186 - 58 = 128
Đáp số: ...