 giúp với ạ
giúp với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\ge-\dfrac{1}{4}\)
- Với \(-\dfrac{1}{4}\le x\le0\Rightarrow\left\{{}\begin{matrix}x^4< \dfrac{1}{4^4}< 1\\\sqrt[4]{4x+1}\ge0\Rightarrow4\sqrt[4]{4x+1}+1\ge1\end{matrix}\right.\)
\(\Rightarrow x^4< 4\sqrt[4]{4x+1}+1\) nên pt vô nghiệm
- Với \(x>0\):
Đặt \(\sqrt[4]{4x+1}=a>0\Rightarrow4x+1=a^4\)
Ta được hệ:
\(\left\{{}\begin{matrix}x^4=4a+1\\a^4=4x+1\end{matrix}\right.\)
Trừ vế cho vế:
\(\Rightarrow x^4-a^4=4\left(a-x\right)\)
\(\Leftrightarrow\left(x-a\right)\left(x+a\right)\left(x^2+a^2\right)+4\left(x-a\right)=0\)
\(\Leftrightarrow\left(x-a\right)\left[\left(x+a\right)\left(x^2+a^2\right)+4\right]=0\)
\(\Leftrightarrow x=a\) (do \(\left(x+a\right)\left(x^2+a^2\right)+4>0\) với \(a;x>0\))
\(\Leftrightarrow x=\sqrt[4]{4x+1}\)
\(\Leftrightarrow x^4=4x+1\)
\(\Leftrightarrow x^4-4x-1=0\)
\(\Leftrightarrow\left(x^4+2x^2+1\right)-\left(2x^2+4x+2\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)^2-2\left(x+1\right)^2=0\)
\(\Leftrightarrow x^2+1=\sqrt{2}\left(x+1\right)\) (do \(x>0\) nên chỉ có TH này xảy ra khi khai căn)
\(\Leftrightarrow x^2-\sqrt{2}x+1-\sqrt{2}=0\)
Pt bậc 2 bình thường, em có thể tính delta và giải theo công thức nghiệm

Gọi số lớn là x, số nhỏ là y
Do hiệu 2 số là 272 nên ta có pt:
\(x-y=272\) (1)
Do số lớn chia số nhỏ được 4 dư 56 nên:
\(x=4y+56\Leftrightarrow x-4y=56\) (2)
Từ (1) và (2) ta được hệ:
\(\left\{{}\begin{matrix}x-y=272\\x-4y=56\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=344\\y=72\end{matrix}\right.\)
Đặt \(x\) là số nhỏ
\(\Rightarrow\) Số lớn \(=4x+56\)
Khi đó, ta có: \(4x+56-x=272\) và ta tìm được \(x=72\)
Nên số lớn là \(344\)
Vậy hai số đó là \(72\) và \(344\)

ĐKXĐ: \(x\ge-\dfrac{1}{3}\)
\(\Leftrightarrow\left(x+1\right)^3+\left(x+1\right)=\left(3x+1+1\right)\sqrt{3x+1}\)
Đặt \(\left\{{}\begin{matrix}x+1=a\\\sqrt{3x+1}=b\ge0\end{matrix}\right.\)
Pt trở thành:
\(a^3+a=\left(b^2+1\right)b\)
\(\Leftrightarrow a^3-b^3+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2+1\right)=0\)
\(\Leftrightarrow a-b=0\) (do \(a^2+ab+b^2+1=\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}+1>0\))
\(\Leftrightarrow\sqrt{3x+1}=x+1\)
\(\Leftrightarrow3x+1=x^2+2x+1\)
\(\Rightarrow x=\left\{0;1\right\}\)

Với mọi x;y dương ta có:
\(\left(x-y\right)^2\ge0\Leftrightarrow x^2+y^2\ge2xy\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge x^2+y^2+2xy\)
\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow\sqrt{x^2+y^2}\ge\dfrac{x+y}{\sqrt{2}}\)
Áp dụng:
\(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\ge\dfrac{a+b}{\sqrt{2}}+\dfrac{b+c}{\sqrt{2}}+\dfrac{c+a}{\sqrt{2}}=\sqrt{2}\left(a+b+c\right)\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
- Với BĐT bên phải: \(\sqrt{3}\left(a+b+c\right)>\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\)
Áp dụng BĐT Bunhiacopxki:
\(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\le\sqrt{3\left(a^2+b^2+b^2+c^2+c^2+a^2\right)}\)
\(\Leftrightarrow\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\le\sqrt{6\left(a^2+b^2+c^2\right)}\)
Nên ta chỉ cần chứng minh:
\(\sqrt{3}\left(a+b+c\right)>\sqrt{6\left(a^2+b^2+c^2\right)}\)
\(\Leftrightarrow\left(a+b+c\right)^2>2\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow a^2+b^2+c^2< 2ab+2bc+2ca\)
Thật vậy, do a, b, c là 3 cạnh của 1 tam giác nên theo BĐT tam giác:
\(\left\{{}\begin{matrix}a< b+c\\b< c+a\\c< a+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2< a\left(b+c\right)\\b^2< b\left(c+a\right)\\c^2< c\left(a+b\right)\end{matrix}\right.\)
Cộng vế:
\(a^2+b^2+c^2< 2ab+2bc+2ca\) (đpcm)

Sửa lại Gia đình bà Vân gồm 4 người lớn và 3 trẻ em thanh toán \(110000\) đồng thành \(1100000\) đồng
Gọi giá buffet của người lớn và trẻ em lần lượt là \(x;y\left(x;y>0\right)\)
Tổng số tiền ông Khanh : \(5x+5y=1500000\)
\(\Rightarrow x+y=300000\left(2\right)\)
Tổng số tiền nhà bà Vân : \(4x+3y=1100000\left(2\right)\)
\(\left(1\right);\left(2\right)\) ta có HPT :
\(\left\{{}\begin{matrix}x+y=300000\\4x+3y=1100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+4y=1200000\\4x+3y=1100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=300000\\y=100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=200000\\y=100000\end{matrix}\right.\)
Vậy giá buffet của người lớn và trẻ em lần lượt là \(200000\left(đồng\right);100000\left(đồng\right)\)
Em kiểm tra lại đề, rất có thể ở dữ liệu nhà bà Vân em ghi thiếu 1 số 0 ở con số 110 000, lẽ ra phải là 1 100 000 mới hợp lý

Câu 2:
a: \(cosa=0\)
=>\(a=90^0\)
b: \(tana=\dfrac{\sqrt{3}}{3}\)
=>\(a=arctan\left(\dfrac{\sqrt{3}}{3}\right)=30^0\)
c: \(cota-sin90^0=0\)
=>\(cota=sin90^0=1\)
=>\(a=45^0\)
d: \(tana=\dfrac{sina}{cota}\)
=>\(\dfrac{sina}{cosa}=\dfrac{sina}{cota}\)
=>\(cota=cosa\)
=>\(cosa\left(\dfrac{1}{sina}-1\right)=0\)
=>\(\left[{}\begin{matrix}cosa=0\\sina=1\end{matrix}\right.\Leftrightarrow a=90^0\)

\(\left(a+1\right)^2-2a-2\)
\(=a^2+2a+1-2a-2=a^2-1< =0\)(Do \(a^2< =1\))
=>\(\left(a+1\right)^2< =2a+2\)
Vì a2 ≤ 1 ⇒ a2 + 1 ≤ 1 + 1 = 2
⇒ a2 + 1 + 2a ≤ 2 + 2a ⇒ (a + 1)2 ≤ 2(đpcm)

Gọi chiều rộng ban đầu là x(m)
(Điều kiện: \(0< x< \dfrac{35}{2}\))
Chiều dài ban đầu là 35-x(m)
Chiều dài sau khi giảm đi 5m là 35-x-5=30-x(m)
Diện tích nhỏ hơn ban đầu là 75m2 nên ta có:
x(35-x)-x(30-x)=75
=>\(35x-x^2-30x+x^2=75\)
=>5x=75
=>x=15(nhận)
Vậy: Chiều rộng ban đầu là 15m
Chiều dài ban đầu là 35-15=20m
Diện tích ban đầu là \(15\cdot20=300\left(m^2\right)\)
Gọi chiều dài và chiều rộng của khu vườn hình chữ nhật lúc đầu lần lượt là `x` và `y (m)`
Điều kiện: `0 <x,y < 35`
Do Khu vườn hình chữ nhật có tổng chiều dài và chiều rộng là 35m
`=> x+y = 35 (1)`
Do nếu giảm chiều dài 5m và giữ nguyên chiều rộng thì diện tích vườn nhỏ hơn lúc đầu là `75m^2` nên
`xy - (x-5)y = 75`
`=> xy -xy +5y = 75`
`=> 5y = 75
`=> y = 15`
Khi đó: `x = 35 - 15 = 20` (Thỏa mãn)
Diện tích khu vườn ban đầu là:
`xy = 20 . 15 = 300 (m^2)`
Vậy diện tích khu vườn ban đầu là `300m^2`

Gọi số lớn là x; số bé là y
Hiệu của hai số là 272 nên x-y=272
Lấy số lớn chia số nhỏ thì được thương là 4, dư là 16 nên x=4y+16
x-y=272
=>4y+16-y=272
=>3y=256
=>\(y=\dfrac{256}{3}\)
\(x=4\cdot\dfrac{256}{3}+16=\dfrac{1072}{3}\)
Gọi số nhỏ là \(x\); \(x\in\) N
Khi đó, số lớn là: \(x\) + 272
Theo bài ra ta có phương trình: \(x\) + 272 = 4\(x\) + 16
4\(x\) - \(x\) = 272 - 16
3\(x\) = 256
\(x\) = 256 : 3
\(x\) = \(\dfrac{256}{3}\) (loại)
Vậy không có hai số tự nhiên nào thỏa mãn đề bài.
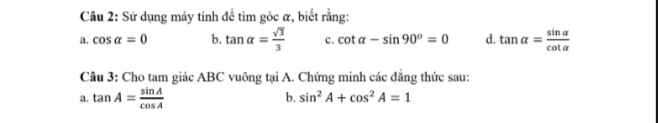
4.
a.
Áp dụng đẳng thức: \(sin^2\alpha+cos^2\alpha=1\)
\(\Rightarrow\left(\dfrac{1}{3}\right)^2+cos^2\alpha=1\)
\(\Rightarrow cos^2\alpha=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
\(\Rightarrow cos\alpha=\dfrac{2\sqrt{2}}{3}\) (do \(\alpha\) nhọn nên \(cos\alpha>0\))
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{1}{3}:\dfrac{2\sqrt{2}}{3}=\dfrac{\sqrt{2}}{4}\)
b.
\(P=sin^21^0+sin^289^0+sin^22^0+sin^288^0+...+sin^244^0+sin^246^0+sin^245^0+sin^290^0\)
\(=sin^21^0+sin^2\left(90^0-1^0\right)+sin^22^0+sin^2\left(90^0-2^0\right)+...+sin^244^0+sin^2\left(90^0-44^0\right)+\left(\dfrac{\sqrt{2}}{2}\right)^2+1^2\)
\(=sin^21^0+cos^21^0+sin^22^0+cos^22^0+...+sin^244^0+cos^244^0+\dfrac{3}{2}\)
\(=1+1+...+1+\dfrac{3}{2}\) (có 44 số 1)
\(=44+\dfrac{3}{2}=\dfrac{91}{2}\)
c.
\(\dfrac{1-tan\alpha}{1+tan\alpha}=\dfrac{1-\dfrac{sin\alpha}{cos\alpha}}{1+\dfrac{sin\alpha}{cos\alpha}}=\dfrac{\dfrac{cos\alpha-sin\alpha}{cos\alpha}}{\dfrac{cos\alpha+sin\alpha}{cos\alpha}}=\dfrac{cos\alpha-sin\alpha}{cos\alpha+sin\alpha}\)