giúp mình với ạ
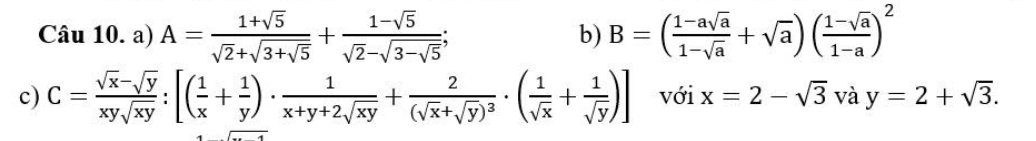
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{13^2-5^2}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot13=5\cdot12=60\)
=>\(AH=\dfrac{60}{13}\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(cosBAH=\dfrac{AH}{AB}=\dfrac{60}{13}:5=\dfrac{12}{13}\)
nên \(\widehat{BAH}\simeq23^0\)


\(\dfrac{1}{1\sqrt{2}+2\sqrt{1}}+\dfrac{1}{2\sqrt{3}+3\sqrt{2}}+...+\dfrac{1}{99\sqrt{100}+100\sqrt{99}}\)
\(=\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}-\dfrac{1}{\sqrt{100}}\)
\(=1-\dfrac{1}{10}=\dfrac{9}{10}\)

\(3\left(x^2+2x-1\right)-2\left(x^2+3x-1\right)+5x^2=0\)
=>\(3x^2+6x-3-2x^2-6x+2+5x^2=0\)
=>\(6x^2-1=0\)
=>\(6x^2=1\)
=>\(x^2=\dfrac{1}{6}\)
=>\(x=\pm\dfrac{\sqrt{6}}{6}\)

a:Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét (O) có \(\widehat{AKB};\widehat{ACB}\) là các góc nội tiếp chắn cung AB
nên \(\widehat{AKB}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{AHE}\left(=90^0-\widehat{DAC}\right)\)
nên \(\widehat{AKB}=\widehat{AHE}\)
=>\(\widehat{AHK}=\widehat{AKH}\)
=>AK=AH
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{FBC}=180^0\)
mà \(\widehat{CEF}+\widehat{AEF}=180^0\)
nên \(\widehat{AEF}=\widehat{ABC}\)
Gọi Ax là tiếp tuyến tại A của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
DO đó: \(\widehat{xAC}=\widehat{ABC}\)
=>\(\widehat{xAC}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên FE//Ax
mà Ax\(\perp\)OA
nên OA\(\perp\)EF

a.
\(\sqrt{x^2-4x+1}=x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2-4x+1=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-4x+1=0\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{1}{4}\)
b.
\(\sqrt{5x^2-2x+2}=x+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1\ge0\\5x^2-2x+2=\left(x+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\4x^2-4x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{1}{2}\)
c.
\(\sqrt{x^2-8x+16}=4-x\)
\(\Leftrightarrow\sqrt{\left(4-x\right)^2}=4-x\)
\(\Leftrightarrow\left|4-x\right|=4-x\)
\(\Leftrightarrow4-x\ge0\)
\(\Rightarrow x\le4\)
d.
\(\sqrt{3x+1}=\sqrt{4x-3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x-3\ge0\\3x+1=4x-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{3}{4}\\x=4\end{matrix}\right.\)
\(\Rightarrow x=4\)

Bài 2:
Xét tam giác ABC vuông tại A ta có:
\(sinC=\dfrac{AB}{BC}=>\dfrac{AB}{BC}=\dfrac{3}{4}\\ =>AB=\dfrac{3}{4}BC=\dfrac{3}{4}\cdot10=\dfrac{15}{2}\left(cm\right)\)
Áp dụng định lý Pythagore cho tam giác ABC ta có:
\(AB^2+AC^2=BC^2\\ =>\left(\dfrac{15}{2}\right)^2+AC^2=10^2\\ =>AC=\sqrt{10^2-\left(\dfrac{15}{2}\right)^2}=\dfrac{5\sqrt{7}}{2}\left(cm\right)\)
Áp dụng hệ thức lượng ta có:
\(AB^2=BC\cdot BH=>BH=\dfrac{AB^2}{BC}=\left(\dfrac{15}{2}\right)^2:10=\dfrac{225}{40}\left(cm\right)\\ AC^2=BC\cdot CH=>CH=\dfrac{AC^2}{BC}=\left(\dfrac{5\sqrt{7}}{2}\right)^2:10=\dfrac{175}{40}\left(cm\right)\)
Bài 9:
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot9\cdot12=54\left(cm^2\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{9}{12}=\dfrac{3}{4}\)
=>\(\dfrac{BD}{BC}=\dfrac{3}{7}\)
=>\(S_{ABD}=54\cdot\dfrac{3}{7}=\dfrac{162}{7}\left(cm^2\right)\)
\(B=\left(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right)^2\)
\(=\left(a+2\sqrt{a}+1\right)\left(\dfrac{1}{1+\sqrt{a}}\right)^2\)
\(=\left(\sqrt{a}+1\right)^2.\dfrac{1}{\left(\sqrt{a}+1\right)^2}=1\)
\(C=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\left(\dfrac{x+y}{xy}\right).\dfrac{1}{\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2}{\left(\sqrt{x}+\sqrt{y}\right)^3}.\left(\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\right)\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\dfrac{x+y}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2}{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\dfrac{x+y}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2\sqrt{xy}}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{x-y}{xy\sqrt{xy}}:\left[\dfrac{x+y+2\sqrt{xy}}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{x-y}{xy\sqrt{xy}}:\left[\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]=\dfrac{x-y}{xy\sqrt{xy}}.xy\)
\(=\dfrac{x-y}{\sqrt{xy}}\)
\(=\dfrac{2-\sqrt{3}-\left(2+\sqrt{3}\right)}{\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}}=\dfrac{-2\sqrt{3}}{\sqrt{4-3}}=-2\sqrt{3}\)
\(A=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{6+2\sqrt{5}}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\sqrt{6-2\sqrt{5}}}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{\left(\sqrt{5}+1\right)^2}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{5}+1}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\left(\sqrt{5}-1\right)}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{3+\sqrt{5}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{3-\sqrt{5}}\)
\(=\sqrt{2}\left(\dfrac{\left(1+\sqrt{5}\right)\left(3-\sqrt{5}\right)+\left(1-\sqrt{5}\right)\left(3+\sqrt{5}\right)}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}\right)\)
\(=\sqrt{2}.\left(\dfrac{-4}{9-5}\right)=-\sqrt{2}\)