Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: \(-\dfrac{18}{31}=\dfrac{-18\cdot114}{31\cdot114}=-\dfrac{2052}{3534}\)
\(-\dfrac{23}{114}=\dfrac{-23\cdot31}{114\cdot31}=\dfrac{-713}{3534}\)
mà -2052<-713
nên \(-\dfrac{18}{31}< -\dfrac{23}{114}\)
b: \(\dfrac{-22}{35}=\dfrac{-22\cdot177}{35\cdot177}=\dfrac{-3894}{6195}\)
\(-\dfrac{103}{177}=\dfrac{-103\cdot35}{177\cdot35}=\dfrac{-3605}{3195}\)
mà -3894<-3605
nên \(-\dfrac{22}{35}< -\dfrac{103}{177}\)
hình như đề bị sai rồi
\(\widehat{CAB}=\widehat{ACM}\) không thể là trung điểm BC được
a: Sửa đề: M là trung điểm của BC
Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A
Xét tam giác ABC:
góc B = góc C
=> tam giác ABC cân tại A
=> AB = AC
Bạn xem lại nhé CM AB=AC mới đúng nha
Ta có, tam giác ABC có góc B bằng góc C
=> Tam giác ABC cân tại A
=>AB=AC
Sửa đề: Tìm x, y nguyên
\(2xy+3y-2x=4\\\Rightarrow (2xy-2x)+(3y-3)=4-3\\\Rightarrow 2x(y-1)+3(y-1)=1\\\Rightarrow (2x+3)(y-1)=1\)
Vì x, y nguyên nên \(\)\(2x+3;y-1\) có giá trị nguyên
Mà \((2x+3)(y-1)=1\)
Do đó ta có bảng sau:
| 2x + 3 | 1 | -1 |
| y - 1 | 1 | -1 |
| x | -1 | -2 |
| y | 2 | 0 |
Vì x, y tìm được đều thoả mãn x, y nguyên nên \((x;y)=(-1;2);(-2;0)\)
$Toru$
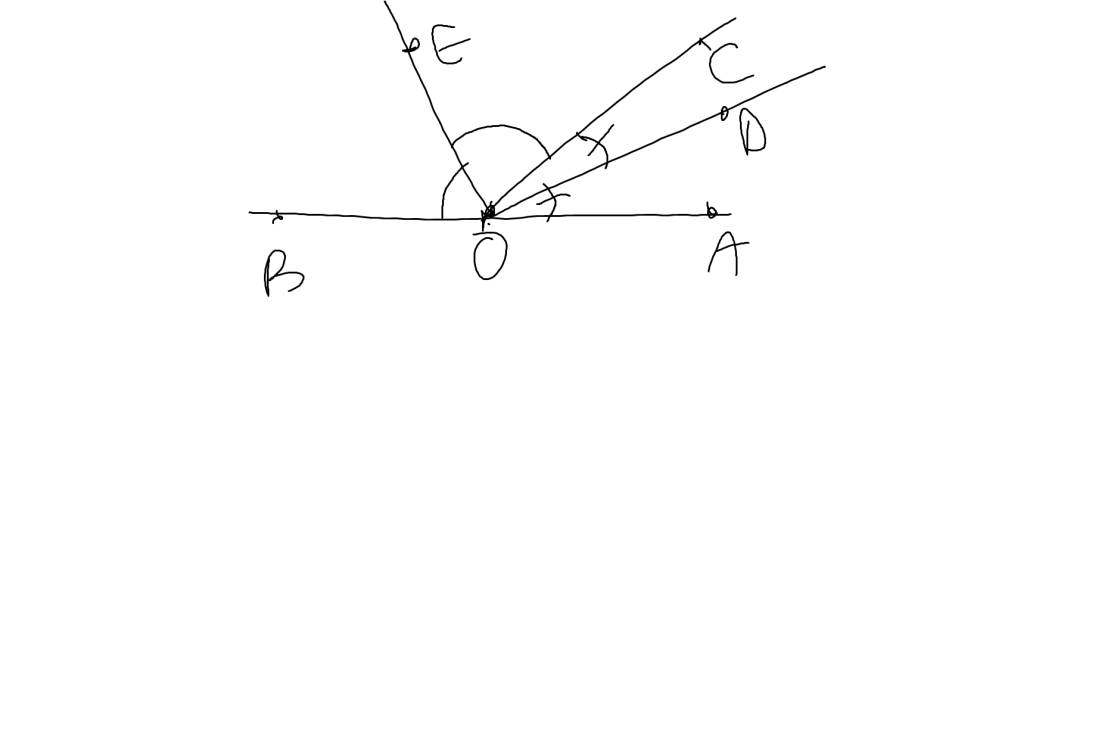
Gọi hai góc kề bù là góc AOC và góc BOC, gọi OD,OE lần lượt là phân giác của góc AOC và góc BOC
OD là phân giác của góc AOC
=>\(\widehat{AOC}=2\cdot\widehat{COD}\)
OE là phân giác của góc BOC
=>\(\widehat{BOC}=2\cdot\widehat{EOC}\)
Ta có: \(\widehat{AOC}+\widehat{BOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{COD}+\widehat{COE}\right)=180^0\)
=>\(2\cdot\widehat{DOE}=180^0\)
=>\(\widehat{DOE}=90^0\)
Đặt: \(A=\dfrac{222}{222^2+1}>0,B=\dfrac{223}{223^2+1}>0\)
Xét:
\(\dfrac{1}{A}=\dfrac{222^2+1}{222}=222+\dfrac{1}{222}\\ \dfrac{1}{B}=\dfrac{223^2+1}{223}=223+\dfrac{1}{223}\)
Dễ dàng nhận thấy: \(\dfrac{1}{A}=222+\dfrac{1}{222}< 222+1< 222+1+\dfrac{1}{223}=\dfrac{1}{B}\)
hay \(\dfrac{1}{A}< \dfrac{1}{B}\Rightarrow A>B\)
Vậy: \(\dfrac{222}{222^2+1}>\dfrac{223}{223^2+1}\)
Bài 4:
a: \(\dfrac{9}{25}=\dfrac{18}{50}>\dfrac{17}{50}\)
=>Số học sinh đi xe buýt nhiều hơn đi xe đạp
b: Số học sinh đi bằng các phương tiện khác chiếm:
\(1-\dfrac{17}{50}-\dfrac{18}{50}=\dfrac{15}{50}\)
Vì \(\dfrac{15}{50}< \dfrac{17}{50}< \dfrac{18}{50}=\dfrac{9}{25}\)
nên số học sinh đi xe buýt là nhiều nhất
Bài 2:
a: \(\dfrac{5}{7}-\dfrac{3}{7}x=1\)
=>\(\dfrac{3}{7}x=\dfrac{5}{7}-1=-\dfrac{2}{7}\)
=>3x=-2
=>\(x=-\dfrac{2}{3}\)
b: \(x-\dfrac{-3}{4}=-\dfrac{14}{25}\)
=>\(x+\dfrac{3}{4}=-\dfrac{14}{25}\)
=>\(x=-\dfrac{14}{25}-\dfrac{3}{4}=\dfrac{-56}{100}-\dfrac{75}{100}=-\dfrac{131}{100}\)
c: \(\dfrac{5}{-20}-x=\dfrac{-7}{5}\)
=>\(x+\dfrac{1}{4}=\dfrac{7}{5}\)
=>\(x=\dfrac{7}{5}-\dfrac{1}{4}=\dfrac{28}{20}-\dfrac{5}{20}=\dfrac{23}{20}\)
d: \(x+\dfrac{3}{4}=\dfrac{36}{144}\cdot\dfrac{-12}{9}\)
=>\(x+\dfrac{3}{4}=\dfrac{1}{4}\cdot\dfrac{-4}{3}=-\dfrac{1}{3}\)
=>\(x=-\dfrac{1}{3}-\dfrac{3}{4}=\dfrac{-13}{12}\)
e: \(\dfrac{8}{23}\cdot\dfrac{46}{24}=\dfrac{1}{3}\cdot x\)
=>\(\dfrac{x}{3}=\dfrac{8}{24}\cdot\dfrac{46}{23}=\dfrac{2}{3}\)
=>x=2
f: \(\dfrac{1}{5}:x=\dfrac{1}{5}-\dfrac{1}{7}\)
=>\(\dfrac{1}{5}:x=\dfrac{2}{35}\)
=>\(x=\dfrac{1}{5}:\dfrac{2}{35}=\dfrac{1}{5}\cdot\dfrac{35}{2}=\dfrac{35}{10}=3,5\)
g: \(\dfrac{4}{9}-\left(x-\dfrac{1}{2}\right)^2=\dfrac{1}{3}\)
=>\(\left(x-\dfrac{1}{2}\right)^2=\dfrac{4}{9}-\dfrac{1}{3}=\dfrac{1}{9}\)
=>\(\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{1}{3}\\x-\dfrac{1}{2}=-\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{6}\\x=\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1}{6}\end{matrix}\right.\)
h: \(3,2x-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):3\dfrac{2}{3}=\dfrac{7}{20}\)
=>\(3,2x-\dfrac{22}{15}:\dfrac{11}{3}=\dfrac{7}{20}\)
=>\(3,2x-\dfrac{22}{15}\cdot\dfrac{3}{11}=\dfrac{7}{20}\)
=>\(3,2x-\dfrac{2}{5}=\dfrac{7}{20}\)
=>\(3,2x=\dfrac{7}{20}+\dfrac{2}{5}=\dfrac{7}{20}+\dfrac{8}{20}=\dfrac{15}{20}=0,75\)
=>x=0,75:3,2=15/64
i: \(\left(4\dfrac{1}{2}-2x\right)\cdot1\dfrac{4}{61}=6\dfrac{1}{2}\)
=>\(\left(\dfrac{9}{2}-2x\right)\cdot\dfrac{65}{61}=\dfrac{13}{2}\)
=>\(\dfrac{9}{2}-2x=\dfrac{13}{2}:\dfrac{65}{61}=\dfrac{13}{2}\cdot\dfrac{61}{65}=\dfrac{61}{10}\)
=>2x=4,5-6,1=-1,6
=>x=-0,8
a:
Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A