lời giải kèm hình giúp mik vs ja mik sẽ kb ạ
giúp mik vs ja mik sẽ kb ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


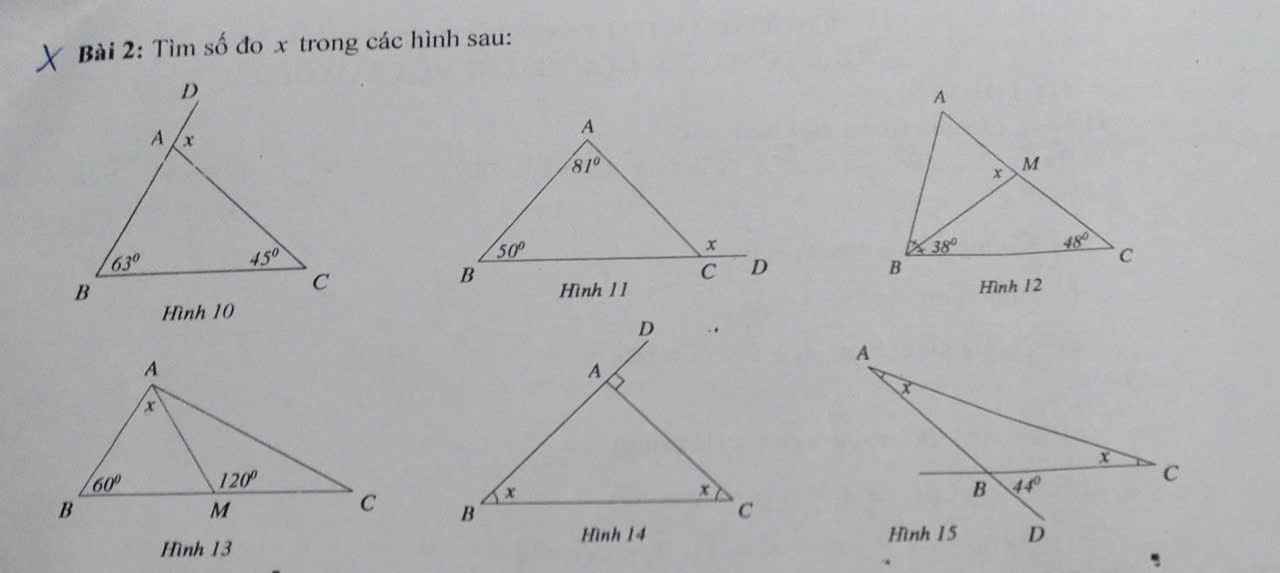
Hình 10: Xét ΔBAC có \(\widehat{CAD}\) là góc ngoài tại đỉnh A
nên \(\widehat{CAD}=\widehat{ABC}+\widehat{ACB}\)
=>\(x=63^0+45^0=108^0\)
Hình 11: Xét ΔABC có \(\widehat{ACD}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACD}=\widehat{CAB}+\widehat{CBA}\)
=>\(x=81^0+50^0=131^0\)
Hình 12: Xét ΔBMC có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{MBC}+\widehat{MCB}\)
=>\(x=38^0+48^0=86^0\)
Hình 13: Xét ΔMAB có \(\widehat{AMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMC}=\widehat{MAB}+\widehat{MBA}\)
=>\(x+60^0=120^0\)
=>\(x=60^0\)
Hình 14: Xét ΔBAC có \(\widehat{CAD}\) là góc ngoài tại đỉnh A
nên \(\widehat{CAD}=\widehat{ABC}+\widehat{ACB}\)
=>\(x+x=90^0\)
=>\(2x=90^0\)
=>\(x=45^0\)
Hình 15:
Xét ΔABC có \(\widehat{CBD}\) là góc ngoài tại đỉnh B
nên \(\widehat{CBD}=\widehat{BAC}+\widehat{BCA}\)
=>\(x+x=44^0\)
=>\(2x=44^0\)
=>\(x=22^0\)

Sau 1 năm, số tiền bác Dũng có:
75000000 + 75000000 . 5,6% = 79200000 (đồng)
Số tiền bác Dũng rút ra:
79200000 : 4 = 19800000 (đồng)
Số tiền bác Dũng còn lại trong ngân hàng:
79200000 - 19800000 = 59400000 (đồng)

\(\dfrac{1}{99}\) - \(\dfrac{1}{99.97}\) - \(\dfrac{1}{97.95}\) - .. - \(\dfrac{1}{3.1}\)
= \(\dfrac{1}{99}\) - (\(\dfrac{1}{99.97}+\dfrac{1}{95.93}+\dfrac{1}{3.1}\))
= \(\dfrac{1}{99}\) - \(\dfrac{1}{2}\) (\(\dfrac{2}{1.3}+\dfrac{2}{3.5}+..+\dfrac{2}{99.97}\))
= \(\dfrac{1}{99}\) - \(\dfrac{1}{2}\)(\(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\))
= \(\dfrac{1}{99}\) - \(\dfrac{1}{2}.\) (\(\dfrac{1}{1}\) - \(\dfrac{1}{99}\))
= \(\dfrac{1}{99}\) - \(\dfrac{1}{2}.\)\(\)\(\dfrac{98}{99}\)
= \(\dfrac{1}{99}\) - \(\dfrac{49}{99}\)
= - \(\dfrac{16}{33}\)

\(\dfrac{9^5-27^3+81^2}{\left(-63\right)}\)
Ta có: \(9=3^2\Rightarrow9^5=\left(3^2\right)^5=3^{10}\)
\(27=3^3\Rightarrow27^3=\left(3^3\right)^3=3^9\)
\(81=3^4\Rightarrow81^2=\left(3^4\right)^2=3^8\)
\(=\dfrac{3^{10}-3^9+3^8}{\left(-63\right)}\)
\(=\dfrac{3^9}{\left(-63\right)}\)
\(=\dfrac{45927}{\left(-63\right)}\)
\(=-729\)
\(\dfrac{9^5-27^3+81^2}{-63}\)
\(=\dfrac{3^{10}-3^9+3^8}{-63}=\dfrac{3^8\left(3^2-3+1\right)}{-63}\)
\(=\dfrac{-3^8\cdot\left(9-3+1\right)}{63}=\dfrac{-3^8}{3^2\cdot7}\cdot7=-3^6\)
=-729

@Nguyễn Thị Thương Hoài
@Nguyễn Lê Phước Thịnh
@Lê Minh Vũ
.... Giúp em với ạ!!

\(\dfrac{x}{y}=\dfrac{y}{10}=\dfrac{10}{x}=\dfrac{x+y+10}{y+10+x}=1\)
\(\Rightarrow x=y=10\)

2\(^{x-3}\) - 3.2\(x\) + 92 = 0
2\(^{x-3}\) - 3.2\(^{x-3}\).23 + 92 = 0
2\(^{x-3}\).(1 - 3.23) + 92 = 0
2\(^{x-3}\).(1 - 24) + 92 = 0
2\(^{x-3}\).(-23) + 92 = 0
2\(^{x-3}\).(-23) = - 92
2\(^{x-3}\) = - 92 : (-23)
2\(^{x-3}\) = 4
2\(^{x-3}\) = 22
\(x-3\) = 2
\(x=2+3\)
\(x=5\)
Vậy \(x=5\)

Đây là toán nâng cao chuyên đề tính chất chia hết của một tổng, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
A = 102008 + 125
A = \(\overline{1000...00}\) + 125 ( 2008 chữ số 0)
A = \(\overline{1000..125}\) (2008 chữ số 0)
Xét tổng các chữ số của A ta có: 1 + 0 x 2008 + 1 + 2 + 5 = 9 ⋮ 9
⇒ A = \(\overline{100...00125}\) ⋮ 9; Mặt khác A = \(\overline{10...00125}\) ⋮ 5
⇒ A \(\in\) BC(5; 9); 5 = 5; 9 = 32 ⇒ BCNN(5; 9) = 32.5 = 45
⇒ A \(\in\) B(45) ⇒ A = 102008 + 125 ⋮ 45 (đpcm)

\(A=-\dfrac{1}{2}\cdot\dfrac{1}{3}+\dfrac{-1}{3}\cdot\dfrac{1}{4}+...+\dfrac{-1}{19}\cdot\dfrac{1}{20}\)
\(=-\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{19\cdot20}\right)\)
\(=-\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)\)
\(=-\left(\dfrac{1}{2}-\dfrac{1}{20}\right)=-\left(\dfrac{10}{20}-\dfrac{1}{20}\right)=-\dfrac{9}{20}\)
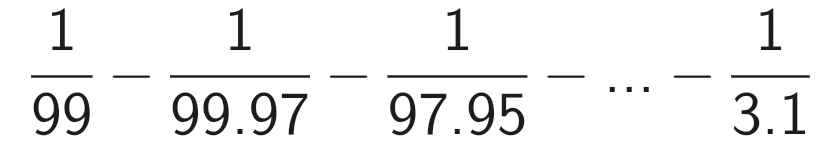
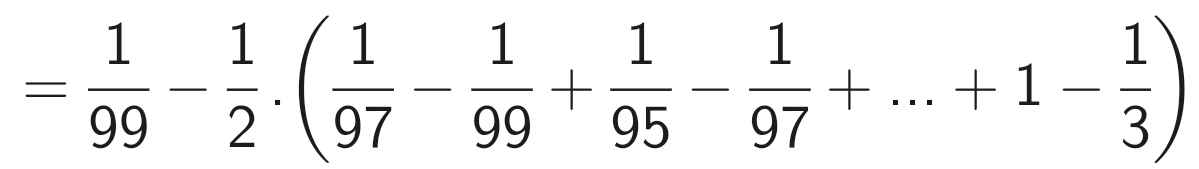
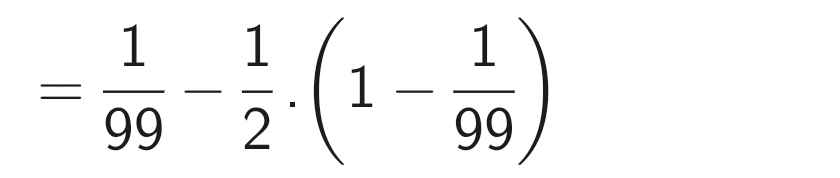
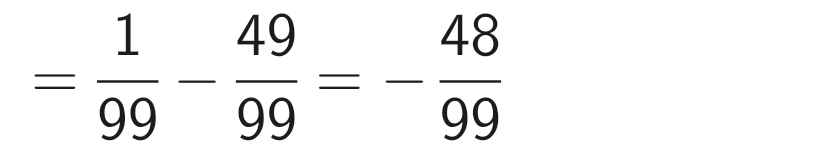
a: Xét ΔMAB và ΔCBA có
\(\widehat{MAB}=\widehat{ABC}\)(hai góc so le trong, MA//BC)
AB chung
\(\widehat{ABM}=\widehat{BAC}\)(hai góc so le trong, MB//AC)
Do đó;ΔMAB=ΔCBA
Xét ΔABC và ΔCNA có
\(\widehat{BAC}=\widehat{NCA}\)(hai góc so le trong, BA//CN)
AC chung
\(\widehat{BCA}=\widehat{NAC}\)(hai góc so le trong, AN//BC)
Do đó: ΔABC=ΔCNA
b: ΔMAB=ΔCBA
=>MA=CB
ΔABC=ΔCNA
=>BC=NA
mà BC=AM
nên AM=AN
mà M,A,N thẳng hàng
nên A là trung điểm của MN