Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Thể tích khối chóp có mặt bên vuông góc với đáy SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
1. Công thức
+ Thể tích khối lăng trụ
$V = S.h$
+ Thể tích khối chóp
$V=\dfrac 13 .S.h$
trong đó, $S$ là diện tích một đáy;
$h$ là chiều cao khối lăng trụ và khối chóp.
4. Khối chóp có mặt bên vuông góc với mặt phẳng đáy
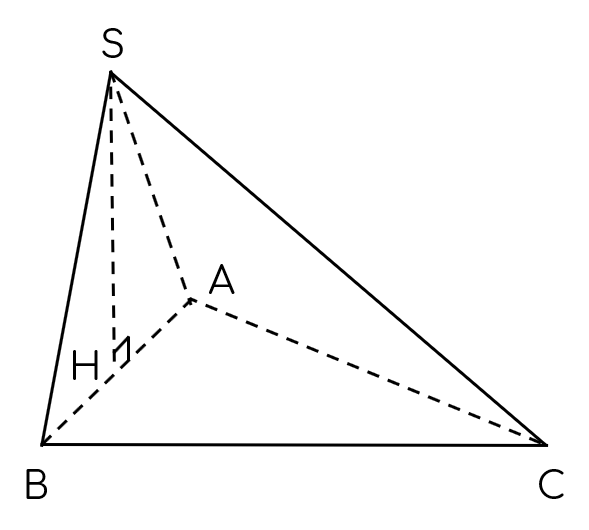
$(SAB)$ vuông góc với $(ABC)$ với giao tuyến là $AB$ thì
đường thẳng $SH$ thuộc mặt phẳng $(SAB)$ vuông góc với giao tuyến chính là đường cao của khối chóp đã cho.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):

Ta có (SAB)⊥(ABC);
Giao tuyến của (SAB) và (ABC) là AB;
SH⊥AB tại H;
SH thuộc mặt phẳng (SAB) thì
SA⊥(SAB).
SH⊥(SAB).
SH⊥SC.
SH⊥(ABC).
Câu 2 (1đ):

Tam giác SAB đều với SB=a và H là trung điểm của AB thì SH bằng
23.
2a3.
4a3.
43.
Câu 3 (1đ):

Đọ dài đoạn BC là
2.
2a.
a2.
2a2.
Câu 4 (1đ):

Với chiều cao SH=2a3 và diện tích tam giác ABC là 2a2.2.
Thể tích khối chóp S.ABC là
12a6.
4a6.
12a36.
4a36.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- cho
- hai ví dụ hỏi chấm một hỏi chấm hai cho
- ta 2 cách để xác định chiều cao của khối
- chóp hỏi chấm a sẽ là một cách tiếp theo
- khi mà thầy cho một hình chóp có mặt bên
- vuông góc với đáy thì chiều cao sẽ được
- xác định như thế nào hỏi chấm 3 hình
- chóp SABC có đáy là một tam giác vuông
- tại B
- cho tam giác SABC đều và thuộc mặt phẳng
- vuông góc với ABC
- a cho các kích thước AB = a AC = a căn 3
- yêu cầu tính thể tích của khối chóp đã
- cho
- I đặc điểm của bài toán này đó là hết AB
- một mặt bên thuộc mặt phẳng vuông góc
- với đáy
- ở khối chóp chúng ta của đáy ABC khi
- mình s sẽ xác định như thế nào để vẽ nửa
- khối chóp này
- Ừ thì các em chú ý vào giả thiết tam
- giác SABC đều s.abe là tam giác đều thì
- gọi H là trung điểm của AB ta sẽ có SH
- vừa là trung tuyến vừa là đường cao hay
- SH vuông góc với AB tại H
- Anh pha giả thiết thứ hai tam giác SAB
- thuộc mặt phẳng vuông góc với mặt phẳng
- ABC hai mặt phẳng SAB vuông góc với mặt
- phẳng ABC phẩy nước lạnh kiến thức của
- lớp 11 nếu như chúng ta có mặt phẳng
- Alpha vuông góc với mặt phẳng beta giao
- tuyến của 2 mặt phẳng này là đường màu
- đỏ khi đó một đường thẳng thuộc vào mặt
- phẳng Alpha mà vuông góc với giao tuyến
- thì sẽ vuông góc với mặt phẳng beta
- Ừ mai toán của chúng ta cũng tương tự
- mặt phẳng SBC và mặt phẳng ABC vuông góc
- với nhau Cây cỏ SH vuông góc với AB tại
- H trong đó
- a a b chính là giao tuyến của mặt phẳng
- SAB và ABC SH vuông góc với giao tuyến
- mà SH lại thuộc vào mặt phẳng s AB sau
- đó SH phẳng vuông góc với mặt phẳng đáy
- ABC
- lịch thi đấu ta sẽ có cách để vẽ chính
- xác khối chóp SABC như sau đầu tiên là
- vẽ đáy ABC trước sau đó lấy H là trung
- điểm của AB từ hát chúng ta sự thẳng
- đứng ta sẽ xác định được đỉnh s nối ssbc
- ta đã có hình chóp SABC có mặt bên SAB
- vuông góc với đáy ABC
- ở Hoa Kỳ đỏ SH chúng ta chính là chiều
- cao của khối chóp
- Ừ như vậy đầu tiên thầy và các em sẽ đi
- tính chiều cao này có giá trị là bao
- nhiêu SH vuông góc với ABC sẽ AB như thế
- này để chúng ta sẽ quan sát
- SBC là tam giác đều có cạnh a SH vuông
- góc với AB h chính là trung điểm của AB
- do đó BH sẽ có độ dài là a trên 2 sử
- dụng Pitago trong tam giác vuông SHB kèm
- máy tính cho thầy SH có giá trị là bao
- nhiêu nhất
- Bình chỉ là a bình phương Chiều Ly a
- bình trên 4 nên SH Bình chỉ là 3/4 a
- bình phương hai SH = a căn 3 trên 2 như
- vậy chiều cao chúng ta đã tính sau tiếp
- theo Đến diện tích đáy diện tích đáy
- chính là diện tích tam giác ABC a a b c
- Đây là một tam giác vuông tại B và có AC
- = a căn 3 a AB = a
- em có nhiều cách để tính diện tích thành
- phần này cụ thể bài này hay sẽ sử dụng
- trực tiếp diện tích tam giác bằng 1/2
- nhân với hai cạnh góc vuông chỉ bằng 1/2
- ab x BC
- Ừ thì chúng ta sẽ cần phải tính xem PC
- có giá trị bằng bao nhiêu
- vẫn sử dụng Pitago trong tam giác vuông
- ta tính được PC và thay vào công thức
- 1/2 AB nhận DC ta sẽ có
- a a
- là Abe nhân acăn2 chỉ là BC tất cả chị
- hai và diện tích đáy là a bình căn 2
- trên 2
- Cho tứ diện tích đáy từ chiều cao em cho
- thầy biết thể tích của khối chóp sẽ bằng
- có nhiều
- thể tích của khối chóp SABC sẽ bằng 1/3
- SH nhân với diện tích tam giác ABC pha
- kết quả của chúng ta sẽ là a mũ 3 căn
- 6/12
- Ừ như vậy quả 3 ví dụ ta đã có ba giọng
- bài khác nhau mỗi Dạo này sẽ lại có một
- cách để chúng ta xác định chiều cao xác
- định đỉnh của khối chóp là khác nhau fan
- chú ý thực hành thêm nhiều dạng bài Hơn
- nữa trên phần luyện tập của org.vn ngoài
- ra chúng ta sẽ còn có một cách để tính
- thể tích của khối chóp cũng như khối
- lăng trụ bằng việc sử dụng tỷ số mà ta
- sẽ học ở bãi tiếp theo bài học của chúng
- ta sẽ kết thúc ở đây Cảm ơn sự theo dõi
- của các em và hẹn gặp lại các em trong
- các bài học tiếp theo trên org.vn
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây