Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
1. Công thức
+ Thể tích khối lăng trụ
$V = S.h$
+ Thể tích khối chóp
$V=\dfrac 13 .S.h$
trong đó, $S$ là diện tích một đáy;
$h$ là chiều cao khối lăng trụ và khối chóp.
2. Khối chóp có cạnh bên vuông góc với mặt phẳng đáy
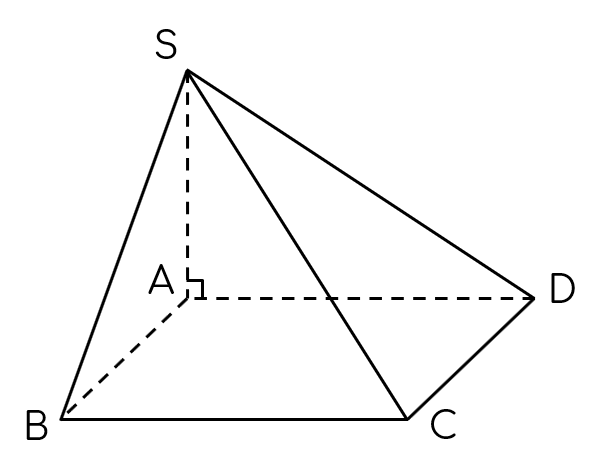
$SA$ vuông góc với $(ABCD)$ thì độ dài của $SA$ chính là chiều cao của khối chóp $S.ABCD$.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Khối lăng trụ ABC.A′B′C′ có diện tích tam giác ABC bằng S
và chiều cao bằng h. Thể tích khối lăng trụ đã cho là
V=S+h.
V=3.S.h.
V=S.h.
V=hS.
Câu 2 (1đ):

Khối chóp S.ABCD có cạnh bên SA vuông góc với mặt phẳng đáy.
Chiều cao khối chóp đã cho là độ dài đoạn
SD.
SB.
SA.
SC.
Câu 3 (1đ):

Ta có: SA=2a;
SABCD=2a2;
Thể tích khối chóp S.ABCD là
V=4a3.
V=34a.
V=34a3.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin
- [âm nhạc]
- [Vỗ tay]
- [âm nhạc]
- chào mừng Cái nó quay trở lại với khóa
- học của lớp 12
- đêm nay chúng ta lại tiếp tục những bài
- học liên quan tới thể tích của các khối
- đa diện và sau của lăng trụ đứng cũng
- như khối lăng trụ xiên khi chúng ta sẽ
- có thể tích khối tiếp theo đó là khối
- chóp hình ảnh của khối chóp chúng ta đã
- gặp rất nhiều trong cuộc sống chúng ta
- cùng nhắc lại một số yếu tố của khối
- chóp nhỏ nhất đầu tiên là về cạnh bên
- thì Esse SB SD Người ta gọi đó là các
- cạnh bên của hình chóp SABCD ABCD ở đây
- chính là mặt đáy của khối chóp phạt
- Ừ chiều cao của khối chóp người ta sẽ
- tính bằng khoảng cách từ đỉnh cho đến
- mặt phẳng đáy đỉnh ở đây là đỉnh s nên
- khoảng cách từ s đến mặt phẳng ABCD
- chính là chiều cao của khối chóp
- khi phát từ các yếu tố này chúng ta sẽ
- đi tìm hiểu thể tích của chó sẽ được
- tính theo công thức nào trước đó Thấy sẽ
- có sự so sánh giữa khối chóp và khối
- lăng trụ về thể tích chúng ở trong hình
- ảnh và kem chuẩn bị theo dõi thì một
- chiếc cấu hình chóp có đáy là một hình
- vuông và một chiếc + hình lăng trụ cũng
- có đáy là hình vuông lượng nước mà hai
- chiếc cốc này chứa được sẽ tương ứng cho
- thể tích của khối chóp và khối lăng trụ
- đứng ở đây đáy của chúng là bằng nhau và
- chiều cao của chúng cũng sẽ bằng nhau
- lý do hai chiếc cốc này có bây giờ đây
- sau đó chiều cao sẽ không tính phần bề
- dày đó cách làm chúng ta như sau
- em thấy sẽ đổ đầy nước vào chiếc cốc
- hình chóp
- sâu đỏ đổ nước đỏ phản hồi trước cốc thì
- lăng trụ
- và kem chú ý Nếu thay đổi lần thứ ba thì
- thể tích của chiếc cốc thì lăng trụ này
- sẽ như thế nào
- Thì đó chiếc cốc thì làm chúng ta sau ba
- lần đầu sẽ chứa đầy nước Hãy chúng ta sẽ
- đưa ra được một nhận xét thể tích của
- khối lăng trụ sẽ gấp 3 lần thể tích của
- một khối chóp mà có cùng kích thước đáy
- cũng như có cùng chiều cao và người ta
- chứng minh được mối liên hệ giữa công
- thức tính thể tích của khối lăng trụ với
- một khối chóp về sau ở đây thầy cho khối
- lăng trụ có đáy ABC và chiều cao là h
- Khi đó thể tích
- như bài học trước chúng ta sẽ có cái
- bằng S nhân hạt em từ đây là diện tích
- của tam giác ABC bây giờ nếu một khối
- chóp cũng có đáy là ABC và chiều cao của
- mực hát thì thể tích sẽ bằng
- 1/3 diện tích đáy nhân với chiều cao
- Ừ như vậy khác biệt giữa 2 công thức
- chính là Hằng Số 1 phần 3 ở đây s chỉ là
- diện tích đáy và trong ví dụ cụ thể này
- là diện tích tam giác ABC còn H là chiều
- cao của khối chóp
- Ừ chiều cao được xác định là khoảng cách
- từ đỉnh cho đến mặt phẳng Đáy
- Ừ như vậy để tính được thể tích của một
- khối chóp lần lượt ta sẽ đi tính diện
- tích này sau đó xác định chiều cao và
- chú ý do thầy hàng số 1 phần 3 thể tích
- bằng 1/3 diện tích đáy nhân với chiều
- cao sử dụng công thức này chúng ta sẽ đi
- vào một số ví dụ cụ thể ở ví dụ đầu tiên
- thì sẽ cho bài toán về hình chóp có cạnh
- bên vuông góc với này hỏi chấm 1 Cho
- hình chóp S.ABCD có đáy là hình chữ nhật
- có kích thước AB bằng a BC bằng 2a và SA
- = 2a trong nó SA vuông góc với mặt phẳng
- đáy yêu cầu tính thể tích của khối chóp
- đã cho
- Cho hình chóp mũi tên có cạnh Bình vuông
- góc với đáy vậy cách vẽ sẽ như thế nào
- trước tiên chúng ta vẫn sẽ đái đái a b c
- d đ
- lý do FA vuông góc với đáy nên từ A
- chúng ta dự thẳng đứng
- sau khi đó xác định được đỉnh s
- FA vuông góc với mặt ở đáy nồi SB SD
- ta đã hoàn thành việc vẽ hình chóp s
- ABCD đ
- Ừ để tính thể tích của khối chóp này
- chúng ta sử dụng công thức p = 1/3 SH và
- kem dễ cũng thấy xác định s&h ở đây sẽ
- có giá trị là bao nhiêu nhất
- hết của chúng ta trong giờ này chính là
- diện tích này cụ thể là diện tích của
- hình chữ nhật ABCD con H là chiều cao
- của khối chóp do FA vuông góc mặt phẳng
- đáy lên
- chính là khoảng cách từ S cho đến mặt
- phẳng ABCD do đó hết ta chỉ là chiều cao
- của khối chóp đã cho
- lý do đó bài toán chúng ta sẽ là tỉnh S
- hay tính diện tích của ABCD sau đó tính
- thể tích a đây xả Thiết đã cho bằng hai
- a rồi đó Chiều cao chúng ta là hai ai
- a tiếp theo là diện tích của hình chữ
- nhật ABCD
- ABCD là hình chữ nhật của AB bằng a và
- BC = 2A sử dụng công thức tính diện tích
- hình chữ nhật đó là chiều dài hơn chiều
- rộng chính là ab nhận đề xây đáp án ta
- là hai Hà Bình Phương và kem cho thời
- biết thể tích của khối chóp SABCD trong
- trường này sẽ nào nhiều nhất
- khi chúng ta sẽ thay số đầu tiên 1/3 sau
- đó diện tích ABCD là hai a bình và chiều
- cao là 2a đáp số chúng ta sẽ là 4/3 a mũ
- 3 đây là thể tích của khối chóp trong hồ
- chứa một
- như vậy những bài toán mà đề bài đã cho
- cạnh bên vuông góc với này thì chúng ta
- sẽ xác định ngay khách bên đó chính là
- chiều cao của khối chóp sau đó vì chiều
- cao tìm diện tích đáy và sử dụng công
- thức ta sẽ tính được thể tích của khối
- chóp
OLMc◯2022


Bạn có thể đánh giá bài học này ở đây