Tổng và hiệu của hai vectơ SVIP

1. TỔNG CỦA HAI VECTƠ

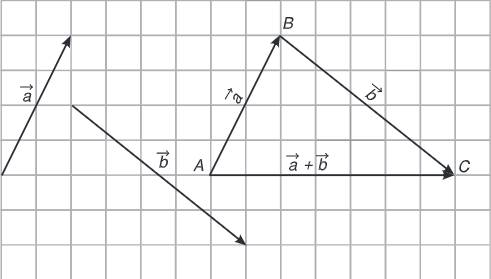
• Cho hai vectơ \(\overrightarrow{a},\overrightarrow{b}\). Lấy một điểm \(A\) tùy ý và vẽ \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{BC}=\overrightarrow{b}\). Khi đó vectơ \(\overrightarrow{AC}\) được gọi là tổng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) và được kí hiệu là \(\overrightarrow{a}+\overrightarrow{b}\).

• Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

• Quy tắc ba điểm: Với ba điểm bất kì \(A,B,C\), ta có \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\).
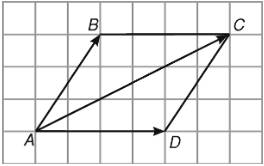
• Quy tắc hình bình hành: Nếu \(ABCD\) là một hình bình hành thì \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}.\)

Tính chất: Với ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) tùy ý:

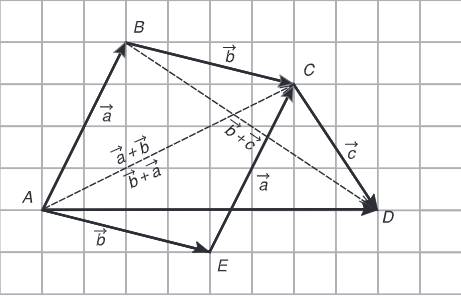
• Tính chất giao hoán: \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\);
• Tính chất kết hợp: \(\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)\);
• Tính chất của vectơ-không: \(\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}.\)

 

 2. HIỆU CỦA HAI VECTƠ

• Vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow{a}\) được gọi là vectơ đối của vectơ \(\overrightarrow{a}\).
• Vectơ đối của vectơ \(\overrightarrow{a}\) được kí hiệu là \(-\overrightarrow{a}\).
• Vectơ \(\overrightarrow{0}\) được coi là vectơ đối của chính nó.

Chú ý: Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng \(\overrightarrow{0}\).

Vectơ \(\overrightarrow{a}+\left(-\overrightarrow{b}\right)\) được gọi là hiệu của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) và được kí hiệu là \(\overrightarrow{a}-\overrightarrow{b}\). Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ 

Chú ý: Nếu \(\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}\) thì \(\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+\left(-\overrightarrow{b}\right)=\overrightarrow{c}+\overrightarrow{b}+\left(-\overrightarrow{b}\right)=\overrightarrow{c}+\overrightarrow{0}=\overrightarrow{c}.\)

Quy tắc hiệu: Với ba điểm \(O,M,N\) ta có: \(\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM.}\) 

 Nhận xét:

• Nếu \(I\) là trung điểm của đoạn thẳng \(AB\) thì \(\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\).
• Nếu \(G\) là trọng tâm của tam giác \(ABC\) thì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).

Ví dụ: Cho bốn điểm \(A,B,C,D\). Chứng minh các đẳng thức sau:

a) \(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}\).

b) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}.\)

Giải

a) Ta có \(\overrightarrow{AC}+\overrightarrow{BD}=\left(\overrightarrow{AD}+\overrightarrow{DC}\right)+\left(\overrightarrow{BC}+\overrightarrow{CD}\right)\)

\(=\overrightarrow{AD}+\overrightarrow{BC}+\left(\overrightarrow{DC}+\overrightarrow{CD}\right)\)

\(=\overrightarrow{AD}+\overrightarrow{BC}+\overrightarrow{DD}\)

\(=\overrightarrow{AD}+\overrightarrow{BC}+\overrightarrow{0}\)

\(=\overrightarrow{AD}+\overrightarrow{BC}.\) (đpcm)

b) Xét \(\overrightarrow{AB}-\overrightarrow{CD}-\left(\overrightarrow{AC}-\overrightarrow{BD}\right)\)

\(=\left(\overrightarrow{AB}-\overrightarrow{AC}\right)-\left(\overrightarrow{CD}-\overrightarrow{BD}\right)\)

\(=\overrightarrow{CB}-\left(\overrightarrow{CD}+\overrightarrow{DB}\right)\)

\(=\overrightarrow{CB}-\overrightarrow{CB}=\overrightarrow{0.}\)

Suy ra \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}\) (đpcm).