Tính độ dài của một dây. Tính khoảng cách từ tâm đến dây SVIP

Hướng dẫn giải:

Gọi $I$ là trung điểm của $OA$.

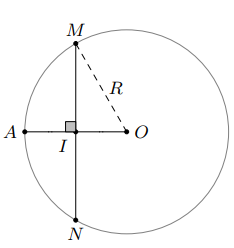
Ta có $OI=\dfrac{1}{2}OA=\dfrac{1}{2}.10=5$

Áp dụng định lí Pythagore vào tam giác vuông $IMO$, ta được:

$IM^2=OM^2-OI^2=10^2-5^2=75$

Suy ra $IM=5\sqrt{3}$.

Ta có $MN \perp OA$ tại trung điểm $I$ của $OA$, nên:

$IM=IN=\dfrac{1}{2}MN$ nên $MN=2IM=2. 5\sqrt{3}=10\sqrt{3}$.

Hướng dẫn giải:

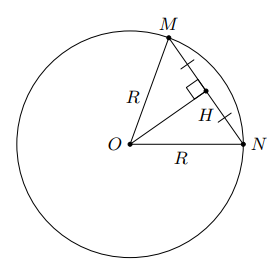
Vẽ $OH \bot MN$ tại $H$ thì $HM=HN=\dfrac{1}{2}MN=\dfrac{R}{2}$.

Áp dụng định lí Pythagore vào tam giác vuông $OMH$, ta được:

$OH^2=OM^2-MH^2=R^2-\Big( \dfrac{R}{2} \Big)^2=\dfrac{3R^2}{4}$

$OH=\sqrt{\dfrac{3R^2}{4}}=\dfrac{R\sqrt3}{2}$

Vậy khoảng cách từ $O$ đến dây $MN$ là $\dfrac{R\sqrt{3}}{2}$.

Hướng dẫn giải:

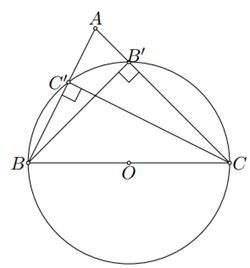
Tam giác $ABC$ có hai đường cao $BB'$ và $CC'$ nên

$\widehat{BC'C}=\widehat{BB'C}=90^\circ $

Suy ra $OB=OC=O{B}'=O{C}'$ (đường trung tuyến ứng với cạnh huyền).

Do đó bốn điểm $B$, $C'$, $B'$, $C$ cùng nằm trên đường tròn tâm $O$ bán kính $OB'$.

Đường kính $BC$, $B'C'$ là dây cung nên độ dài $B'C'$ nhỏ hơn độ dài $BC$.

Hướng dẫn giải:

Tứ giác $ABCD$ có $\widehat{B}=\widehat{D}=90^\circ$ nên $OA=OB=OC=OD$ (trung tuyến ứng với cạnh huyền).

Suy ra bốn điểm $A$, $B$, $C$, $D$ cùng nằm trên một đường tròn tâm $O$, đường kính $AC$.

$AC$ là đường kính, $BD$ là dây không đi qua điểm $O$.

Suy ra $AC>BD$.

Hướng dẫn giải:

Kẻ $OH$ vuông góc với $AB$ tại $H$.

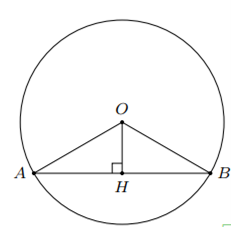
Khi đó $H$ là trung điểm của $AB$ hay $AH=\dfrac{AB}{2}=\dfrac{3}{2}$.

Vì cung nhỏ $\overset\frown{AB}=100^\circ $ nên $\widehat{AOB}=100^\circ $

Hay $\widehat{AOH}=50^\circ $.

Ta có $AO=\dfrac{AH}{\sin \widehat{AOH}}=\dfrac{3}{2\sin 50^\circ }=2$ cm.

Hướng dẫn giải:

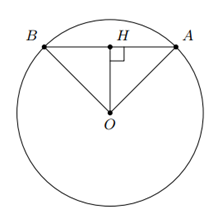
a) Ta có sđ$\overset\frown{AB}_{\text{nhỏ}}+$sđ$\overset\frown{AB}_{\text{lớn}}=360^\circ $,

mà sđ$\overset\frown{AB}_{\text{lớn}}=3$sđ$\overset\frown{AB}_{\text{nhỏ}}$.

Suy ra sđ${{\overset\frown{AB}}_{\text{nhỏ}}}=90^\circ $;

sđ${{\overset\frown{AB}}_{\text{lớn}}}=270^\circ $.

b) Ta có $\widehat{AOB}=$ sđ${{\overset\frown{AB}}_{\text{nhỏ}}}=90^\circ $, mà $OA=OB=R$.

Suy ra tam giác $OAB$ vuông cân tại $O$.

Mặt khác $OH \bot AB=\left\{ H \right\}$.

Suy ra $\Delta OHA$ vuông cân tại $H$ suy ra $OH=HA=\dfrac{AB}{2}$.

Hướng dẫn giải:

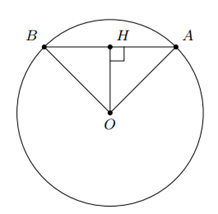
sđ$\overset\frown {AB}_{\text{lớn}}+$sđ$\overset\frown{AB}_{\text{nhỏ}}=360^\circ $,

sđ$\overset\frown{AB}_{\text{lớn}}=2$sđ$\overset\frown{AB}_{\text{nhỏ}}$ nên:

sđ${{\overset\frown{AB}}_{\text{nhỏ}}}=120^\circ $.

Suy ra $\widehat{AOB}=120^\circ $.

Vẽ $OH \bot AB$, ta có $\widehat{AOH}=\widehat{HOB}=60^\circ $ và $AH=HB=\dfrac{1}{2}AB$.

Tam giác $AOH$ có $\widehat{AHO}=90^\circ $, $\widehat{AOH}=60^\circ $ nên

$OH=\dfrac{1}{2}AO=\dfrac{1}{2}R$

Áp dụng định lí Pythagore ta có:

$AH^2=AO^2-OH^2=\dfrac{3R^2}{4}$

Suy ra $AH=\dfrac{R\sqrt{3}}{2}$.

Vậy $AB=2AH=R\sqrt{3}$.