Cung và dây của một đường tròn SVIP

1. Dây và đường kính của đường tròn

a. Khái niệm

🔸Đoạn thẳng nối hai điểm tùy ý của một đường tròn gọi là một dây (hay dây cung) của đường tròn.

🔸Mỗi dây đi qua tâm là một đường kính của đường tròn. Đường kính của đường tròn bán kính $R$ có độ dài bằng $2R$.

Ví dụ 1.

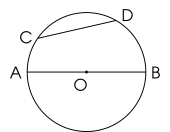
Trong hình trên, CD là một dây; AB là đường kính của $(O)$.

b. Quan hệ giữa dây và đường kính

Trong một đường tròn, đường kính là dây cung lớn nhất.

Ví dụ 2.

AB là dây và CD là đường kính của đường tròn (O ; r) thì AB < CD.

2. Góc ở tâm, cung và số đo của một cung

a. Khái niệm

Cho hai điểm A và B cùng thuộc một đường tròn. Hai điểm ấy chia đường tròn thành hai phần, mỗi phần gọi là một cung tròn. Hai điểm A và B gọi là hai mút của mỗi cung đó.

Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.

Ví dụ 3.

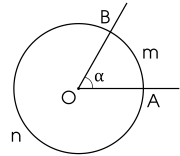
Trong hình vẽ trên, 2 cung: AmB và AnB và 1 góc ở tâm: góc AOB.

Chú ý

🔸Khi góc AOB không bẹt thì cung nằm trong góc AOB gọi là cung nhỏ, cung còn lại gọi là cung lớn.

🔸Khi góc AOB bẹt thì mỗi cung AB được gọi là một nửa đường tròn.

🔸Góc AOB chắn cung AB hay cung AB bị chắn bởi góc AOB.

b. Số đo của một cung

🔸Số đo của nửa đường tròn bằng $180^\circ$.

🔸Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

🔸Số đo của cung lớn bằng hiệu giữa $360^\circ$ và số đo của cung nhỏ có chung hai đầu mút.

Ví dụ 4.

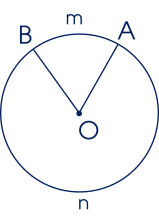
Số đo của cung $AB$ được kí hiệu là sđ$\stackrel\frown{AB}$, ta có:

sđ$\stackrel\frown{AmB}  =  \widehat{AOB} = \alpha$;  sđ$\stackrel\frown{AnB} =  360^\circ- \alpha$.

Lưu ý

🔸Các cung có số đo bằng no được gọi chung là cung $n^\circ$.

🔸Mỗi điểm trên đường tròn là một cung $0^\circ$, cả đường tròn được xem là cung $360^\circ$.

🔸Tổng số đo hai cung có chung đầu mút là $360^\circ$.