Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

$​A=\sqrt{2-\sqrt{3}}.(\sqrt{6}+\sqrt{2})$

$​​A=\sqrt{2}.(\sqrt{2-\sqrt{3}})+\sqrt{6}.(\sqrt{2-\sqrt{3}})$

$A=\sqrt{4-2\sqrt{3}}+\sqrt{12-6\sqrt{3}}$

$A=\sqrt{1+3-2\sqrt{1.3}}+\sqrt{12-2.3\sqrt{3}}$

$A=\sqrt{1^2-2\sqrt{1.3}+(\sqrt{3})^2}+\sqrt{3^2-2.3\sqrt{3}+(\sqrt{3})^2}$

$A=\sqrt{(1-\sqrt{3})^2}+\sqrt{(3-\sqrt{3})^2}$

$A=\sqrt{3}-1+3-\sqrt{3}=2$.

Hướng dẫn giải:

a. Rút gọn biểu thức $A$.

$A=\Bigg(\dfrac{\sqrt{x}+2}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{2-\sqrt{x}}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3} \Bigg):\Bigg(2-\dfrac{\sqrt{x}}{\sqrt{x}+1} \Bigg)$ 

$A=\Bigg(\dfrac{\sqrt{x}+2}{(\sqrt{x}-2)(\sqrt{x}-3)}-\dfrac{\sqrt{x}+3}{2-\sqrt{x}}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3} \Bigg):\Bigg(2-\dfrac{\sqrt{x}}{\sqrt{x}+1} \Bigg)$ 

$A=\Bigg(\dfrac{\sqrt{x}+2}{(\sqrt{x}-2)(\sqrt{x}-3)}+\dfrac{(\sqrt{x}+3)(\sqrt{x}-3)}{(\sqrt{x}-2)(\sqrt{x}-3)}-\dfrac{(\sqrt{x}+2)(\sqrt{x}-2)}{(\sqrt{x}-3)(\sqrt{x}-2)} \Bigg):\Bigg(2-\dfrac{\sqrt{x}}{\sqrt{x}+1} \Bigg)$ 

$A=\dfrac{\sqrt{x}+2+x-9-x+4}{(\sqrt{x}-2)(\sqrt{x}-3)}:\Bigg(2-\dfrac{\sqrt{x}}{\sqrt{x}+1} \Bigg)$ 

$A=\dfrac{\sqrt{x}-3}{(\sqrt{x}-2)(\sqrt{x}-3)}:\dfrac{\sqrt{x}+2}{\sqrt{x}+1}$ 

$A=\dfrac{1}{\sqrt{x}-2}.\dfrac{\sqrt{x}+1}{\sqrt{x}+2}$ 

$A=\dfrac{\sqrt{x}+1}{x-4}$.

b. Tìm các giá trị của x để $\dfrac{1}{A} \le -\dfrac{5}{2}$.

(ĐK: $x\ge 0,x\ne 4,x\ne 9$)

Để $\dfrac{1}{A}\le -\dfrac{5}{2}$ thì

$\dfrac{x-4}{\sqrt{x}+1}\le -\dfrac{5}{2}$

$2x-8\le -5\sqrt{x}-5$

$2x+5\sqrt{x}-3\le 0$

$ -3\le \sqrt{x}\le \dfrac{1}{2}$

$ 0\le \sqrt{x}\le \dfrac{1}{2}$

$ 0\le x\le \dfrac{1}{4}$.

Kết hợp với điều kiện ta được $0\le x\le \dfrac{1}{4}$ thì $\dfrac{1}{A}\le -\dfrac{5}{2}$.

Hướng dẫn giải:

Đổi $1$ giờ $25$ phút $=\dfrac{17}{12}$ giờ; $1$ giờ $30$ phút $=\dfrac{3}{2}$ giờ.

Gọi vận tốc riêng của ca nô và vận tốc của dòng nước lần lượt là $x$ (km/h) và $y$ (km/h). Điều kiện $x>0,\,y>0,\,x>y$.

Trong lần 1

+) Vận tốc xuôi dòng là $x+y$ km/h, quãng đường xuôi dòng là $20$ km nên thời gian xuôi dòng là $\dfrac{20}{x+y}$ (giờ).

+) Vận tốc ngược dòng là $x-y$ km/h, quãng đường ngược dòng là $18$ km nên thời gian ngược dòng là $\dfrac{18}{x-y}$ (giờ).

Vì tổng thời gian xuôi dòng và ngược dòng hết $\dfrac{17}{12}$ giờ nên ta có phương trình

$\dfrac{20}{x+y}+\dfrac{18}{x-y}=\dfrac{17}{12}$     (1)

Trong lần 2

+) Vận tốc xuôi dòng là $x+y$ (km/h), quãng đường xuôi dòng là $15$ km nên thời gian xuôi dòng là $\dfrac{15}{x+y}$ (giờ).

+) Vận tốc ngược dòng là $x-y\,\,(km/h)$, quãng đường ngược dòng là $24$ km nên thời gian ngược dòng là $\dfrac{24}{x-y}$ (giờ).

Vì tổng thời gian xuôi dòng và ngược dòng hết $\dfrac{3}{2}$ giờ nên ta có phương trình

$\dfrac{15}{x+y}+\dfrac{24}{x-y}=\dfrac{3}{2}$    (2)

Từ (1) và (2) ta có hệ phương trình

$\left\{ \begin{aligned}& \dfrac{20}{x+y}+\dfrac{18}{x-y}=\dfrac{17}{12} \\& \dfrac{15}{x+y}+\dfrac{24}{x-y}=\dfrac{3}{2} \\\end{aligned} \right.$

$\left\{ \begin{aligned}& \dfrac{60}{x+y}+\dfrac{54}{x-y}=\dfrac{17}{4} \\& \dfrac{60}{x+y}+\dfrac{96}{x-y}=\dfrac{7}{4} \\\end{aligned} \right.$

$\left\{ \begin{aligned}& \dfrac{60}{x+y}+\dfrac{54}{x-y}=\dfrac{17}{4} \\& \dfrac{42}{x-y}=\dfrac{7}{4} \\\end{aligned} \right.$

Quy đồng ta được hệ $\left\{ \begin{aligned}& x+y=30 \\& x-y=24 \\\end{aligned} \right.$

Giải hệ trên, ta được: $\left\{ \begin{aligned}& x=27 \\& y=3 \\\end{aligned} \right.$ (thỏa mãn điều kiện).

Vậy vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là $27$ km/h và $3$ km/h.

Hướng dẫn giải:

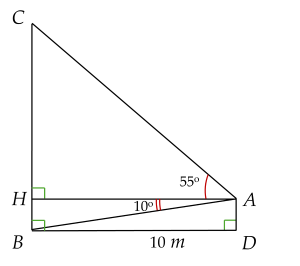
Dựa vào hình vẽ minh họa, ta có: $AH = BD = 10$ m.

Xét $\Delta AHB$ vuông tại $H$, ta có:

$\tan \widehat{BAH}=\dfrac{BH}{AH}$ (tỉ số lượng giác của góc nhọn)

suy ra $BH=AH.\tan \widehat{BAH}=10.\tan 10^\circ$ (m).

Xét $\Delta AHC$ vuông tại $H$, ta có:

$\tan \widehat {CAH}=\dfrac{CH}{AH}$ (tỉ số lượng giác của góc nhọn)

suy ra $CH=AH.\tan\widehat{CAH}=10.\tan 55^\circ$ (m).

Ta có: $BC=BH+CH=10.\tan 10^\circ+10.\tan 55^\circ \approx 16$ m.

Vậy chiều cao của tháp là $16$ m.

Hướng dẫn giải:

Gọi $x$ là số máy in mà nhà xuất bản sử dụng $(1\le x \le 14)$.

Chi phí lắp đặt là $120x$ (nghìn đồng).

Số giờ để sản xuất đủ số ấn phẩm là: $\dfrac{4 \, 000}{30x}$ (giờ).

Chi phí giám sát là: $90.\dfrac{4 \, 000}{30x}=\dfrac{12 \, 000}{x}$ (nghìn đồng).

Chi phí sản xuất của nhà sản xuất là: $A=120x+\dfrac{12 \, 000}{x}$ (nghìn đồng).

Áp dụng bất đẳng thức Cauchy, ta có:

$A=120x+\dfrac{12 \, 000}{x} \ge 2\sqrt{120x.\dfrac{12 \, 000}{x}}=2\,400$.

Dấu bằng xảy ra khi $120x=\dfrac{12 \, 000}{x}$ hay $x=10$.

Vậy số máy in nhà xuất bản nên sử dụng để chi phí in là nhỏ nhất là $10$ máy.

Hướng dẫn giải:

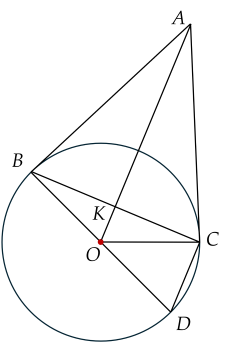
a) Xét tam giác $ABC$ có $AB=AC$ và $AO$ là đường phân giác của góc $BAC$ (tính chất hai tiếp tuyến cắt nhau). Do đó $AO$ cũng là đường cao, đường trung tuyến của $\Delta BAC$.

Vậy $AO$ vuông góc với $BC$.

b) Ta có $\widehat{BDC}=\dfrac12 \stackrel\frown{CB}$ (góc nội tiếp)

$\widehat{BOC}= \stackrel\frown{CB}$ (góc ở tâm)

Mặt khác $\widehat{BAC}=\dfrac12\widehat{BOC}$ nên $\widehat{BAC}=\dfrac12 \stackrel\frown{CB}$.

Vậy $\widehat{BAC}=\widehat{BDC}$, suy ra $OA//CD$ (hai góc đồng vị bằng nhau).

c) Xét tam giác $ABO$ và tam giác $BKO$ có:

$\widehat{ABO}=\widehat{BKO}=90^\circ$

$\widehat{BOA}$: góc chung 

Suy ra $\Delta ABO \sim \Delta BKO$ (g.g).

Do đó ta có tỉ số $\dfrac{AO}{BO}=\dfrac{BO}{KO}$ hay $OA.OK=OB^2=6^2=36$ (cm).

Xét tam giác vuông $ABO$ có: $\sin \widehat{BAO}=\dfrac {OB}{OA}=\dfrac{6}{12}$.

Suy ra $\widehat{BAO}=30^\circ$.