Bài học cùng chủ đề
- Hai đường thẳng song song, chéo nhau
- Luyện tập
- Ôn tập: Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song
- Ôn tập: Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song
- Tham khảo: Một số kinh nghiệm khi làm toán dựng hình
- Ôn tập phần tham khảo: Một số kinh nghiệm khi làm toán dựng hình
- Phiếu bài tập: Hai đường thẳng song song, chéo nhau
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Ôn tập: Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
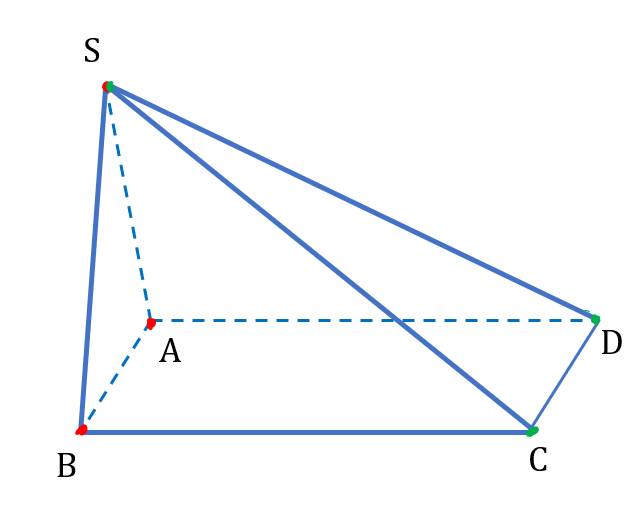
Điểm nào dưới đây thuộc cả hai mặt phẳng (SAB) và (SCD)?
C
D
S
A
Câu 2 (1đ):
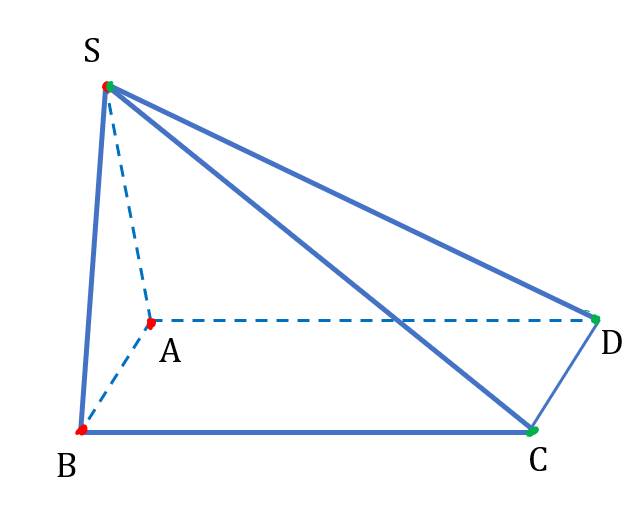
AB và CD là hai đường thẳng
- đồng phẳng.
- không đồng phẳng.
Câu 3 (1đ):
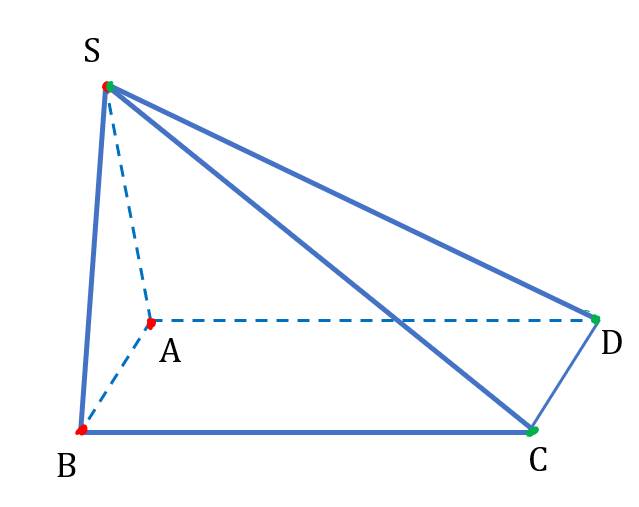
Trong mặt phẳng (ABCD): hai đường thẳng AB và CD
- song song.
- cắt nhau tại một điểm.
Câu 4 (1đ):
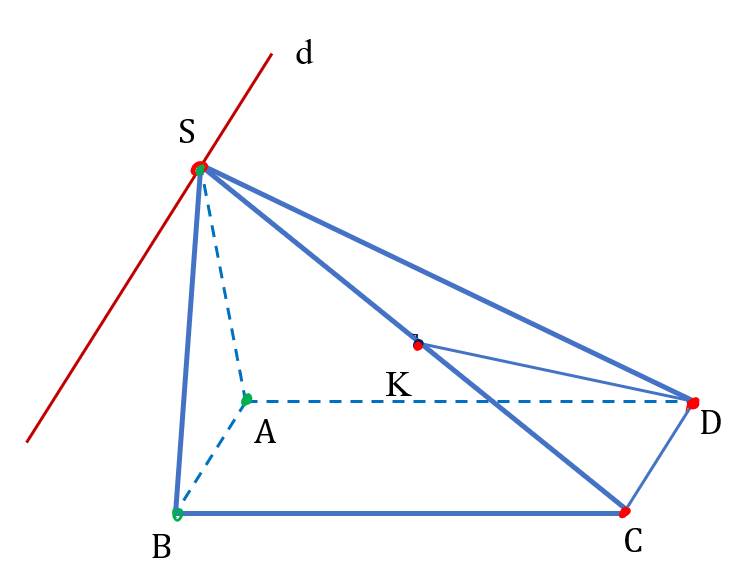
DK nằm trong
(ABCD).
(SAD).
(SCD).
Câu 5 (1đ):
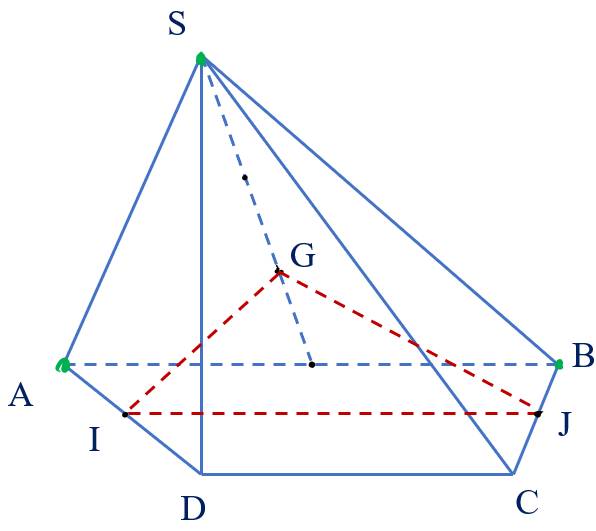
Điểm nào dưới đây thuộc hai mặt phẳng (SAB) và (IJG)?
S.
A.
J.
G.
Câu 6 (1đ):
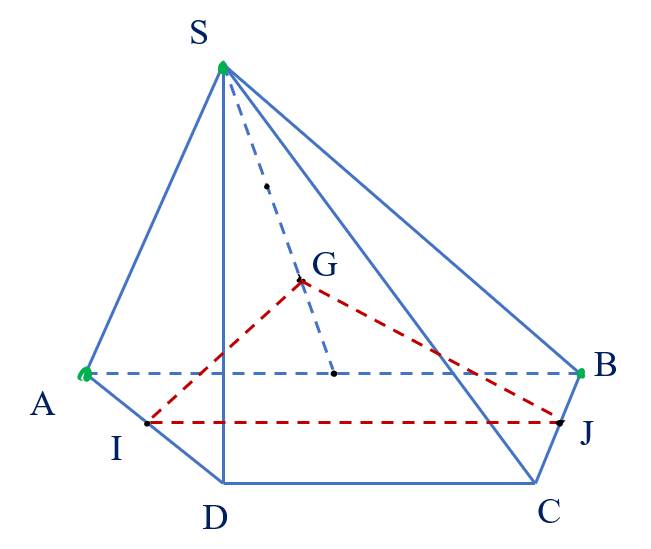
IJ đồng phẳng với đường thẳng nào của mặt phẳng (SAB)?
SB.
SA.
DC.
AB.
Câu 7 (1đ):
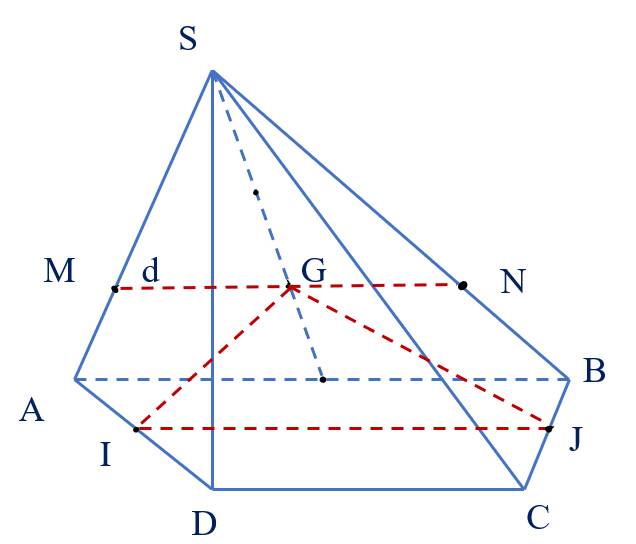
Kéo thả đáp án đúng vào ô trống:
(IJG) ∩ (SAB) =
(IJG) ∩ (SAD) =
(IJG) ∩ (ABCD)=
(IJG) ∩ (SBC) =
NJIJMNMI
(Kéo thả hoặc click vào để điền)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- cho cháu về học sinh tiếp tục một số
- dạng bài tập về quan hệ song song thì
- trong bài giảng lần này chúng ta sẽ đi
- vào bài thứ hai và dạng thứ nhất
- xác định giao tuyến của 2 mặt phẳng chứa
- hai đường thẳng song song
- trước hết thì sẽ nhắc lại một số lý
- thuyết chúng ta cần dùng trong trạng này
- Đầu tiên là mệnh đề trong không gian hai
- đường thẳng song sau thì đồng phẳng
- tức là hình như thấy có hai đường thẳng
- song song
- thì sẽ tồn tại mặt phẳng chứa hai đường
- thẳng song song là
- tiếp theo chúng ta sẽ ếch xanh định lý
- nếu mặt phẳng đôi một cắt nhau chưa bao
- giờ từng phân biệt thì 3 sau từng ấy
- hoặc đồng quy hoặc đôi một song song với
- nhau
- ừ ừ
- anh để hình Dung và định lý này thì chưa
- biết thì cứ bé hai mặt phẳng cắt nhau
- trước
- hai mặt phẳng của chương trình vẽ cắt
- nhau tại sao tuyến này
- nếu mặt phẳng thứ ba à
- khi cắt hai mặt phẳng còn lại theo hướng
- này thì ba giao tuyến của chúng
- ở Ngã Ba Đường Màu đỏ sẽ đồng quy tại 1
- điểm
- cho
- con Nếu mặt phẳng thứ ba cắt hai mặt
- phẳng theo hướng này à
- Ừ thì giao tuyến của chúng sẽ song song
- với nhau
- trực tiếp theo chúng ta sẽ đi vào phần
- Chính cách xác định giao tuyến của 2 mặt
- phẳng chứa hai đường thẳng song song
- ở trên bài giảng thầy có hai mặt phẳng P
- và Q với điểm trong đầu tiên là điểm s
- và thấy có đường thẳng d
- và mặt phẳng P và đường thẳng d phẩy mặt
- phẳng Q song song với nhau
- sau D và D phẩy song song với nhau thế
- nên D vào đây phải đồng phẳng tức là tồn
- tại là khoảng R chứa đường thẳng lên và
- đường thẳng d phải
- đến nay thì ta cùng ai ba mặt phẳng P Q
- R là ba mặt phẳng tôi một cách nhau hơn
- nữa ta có D là giao tuyến của mặt phẳng
- P với mặt phẳng R và đây phẩy là giao
- tuyến của mặt phẳng quy cái mặt phẳng r
- d song song với phận do đó áp dụng định
- lí về ba mặt phẳng đôi một khác nhau thì
- giao tuyến của mặt phẳng P đường thẳng
- quy sẽ song song với D Gọi phẩm và kể từ
- điểm chung đầu tiên
- cá nhân vật các bước xác định giao tuyến
- của 2 mặt phẳng chứa hai đường thẳng
- song song sẽ gần như tương tự đối với
- cách xác định giao tuyến của 2 mặt phẳng
- chúng ta đã học từ bài trước bước đầu
- tiên chúng ta vẫn tìm điểm chung thống
- nhất cụ thể điểm chung ở đây tại điểm s
- tiếp theo chúng ta vẫn chọn ra hai đường
- thẳng đồng phẳng 1 đường nằm trong tay
- của đường nằm trong quy Tuy nhiên ở
- trong trường này chúng ta không chỉ cho
- đi vào đây phải cắt nhau được thì chúng
- song sau
- Khi Gió Đỏ nếu như chúng ta tìm được
- đường thẳng d song song với đường thẳng
- d phẩy mà D nằm trong mặt phẳng P D phẩy
- nằm trong mặt phẳng tôi thì giao tuyến
- cần tìm là đường thẳng đi qua điểm trung
- đầu tiên là điểm s và song song với
- đường thẳng lên đây nóng xong xong đi
- thẳng bên phải
- Ừ nếu vậy chúng ta đã học thêm một
- trường hợp nữa về cách xác định giao
- tuyến của hai mặt phẳng phân điện
- mà cụ thể ở đây là hai mặt phẳng chứa
- hai đường thẳng song song a
- Ừ
- Để hiểu hơn về cách xác định giao tuyến
- của 2 mặt phẳng chứa hai đường thẳng
- song song chúng ta sẽ đi vào một số bài
- tập
- Anh bài 1 yêu cầu chúng ta vẫy hình chóp
- SABCD có đáy ABCD là hình bình hành
- khi chúng ta sẽ đây chóp S.ABCD sao
- câu Ai yêu cầu chúng ta tìm giao tuyến
- của mặt phẳng SAB và SCD
- s a
- a b
- hết ế a c d e
- ừ ừ
- Ê tao thấy hết là điểm trung đầu tiên
- của hai mặt phẳng này
- có mã số sp điểm chung đầu tiên nên
- chúng ta cần phải chết hai đường thẳng
- không sửa điểm s ở trong hai mặt phẳng
- đó là đường thẳng a b
- và đường thẳng CD
- Ê tao thấy đường thẳng AB và đường thẳng
- CD là hai đường thẳng song song cho ABCD
- là hình bình hành sau đó sắc mặt phẳng
- ABCD chúng ta sẽ không để cho AB cắt với
- đường thẳng DC để từ từ Trung thứ hai
- mặt chúng ta sẽ từ điểm s là điểm chung
- nhất
- mấy đường thẳng d song song với đường
- thẳng AB và song song với đường thẳng CD
- ca cổ đường thẳng d chính là giao tuyến
- của mặt phẳng SAB và mặt phẳng SCD
- tiếp theo ta sang câu b d và yêu cầu
- chúng ta Tìm giao điểm của đường thẳng d
- ca với mặt phẳng s AB
- K là trung điểm SC
- thì KC ở đây Tìm giao điểm của đường
- thẳng d ca
- với mặt phẳng SAB
- pk vs
- ê ê
- à à
- Ừ để tìm giao điểm của đường thẳng d ca
- với mặt phẳng SAB thì trước hết chúng ta
- cần phải xem xem đường thẳng d k nằm
- trong mặt phẳng nào
- à à
- Ê
- tao thấy đường thẳng d k nằm trong mặt
- phẳng x d c s c
- có những thằng DK
- tiếp theo là chúng ta cần tìm giao tuyến
- của mặt phẳng SBC với mặt phẳng s AB thì
- danh tiếng này một câu 3 chúng ta đã làm
- rồi nó chính là đường thẳng đen đến đây
- thì chúng ta sẽ cho đường thẳng d k cắt
- với rau tiếng Anh
- trong phẳng SCD cho nick cắt ra tiền lên
- tại điểm H như vậy DK ra với mặt phẳng s
- AB tại điểm H A
- khi tiếp theo chúng ta xanh bài thứ hai
- a
- Mở bài thứ 2 vẽ hình chóp SABCD có đáy
- ABCD là hình thang các cạnh đáy là AB và
- CD
- cho
- SABCD cạnh đáy AB và CD a
- à à
- Ừ chắc Gọi y là trung điểm AB
- và j là trung điểm bc đi là à
- anh mơ G là trọng tâm của tam giác SAB
- anh nói gì à
- hai người đã sống trong tam giác SABC có
- anh đi và yêu cầu chúng ta tìm giao
- tuyến của AB và
- YG
- ta thấy ngay là tiếng Trung thứ nhất của
- hai mặt phẳng s AB và AC theo a
- lý do vừa điểm chung thống nhất thì nên
- chúng ta sẽ không xét những đường thẳng
- chứa điểm cơ ở trong mặt phẳng YG
- cũng thể hơn ở đây chúng ta còn lại
- đường thẳng IV I
- nữ
- DJ đồng phẳng với đường thẳng AB của mặt
- phẳng SAB
- Tuy nhiên ở trong bài này chúng ta cũng
- sẽ không cho IV cắt với đường thẳng AB
- được
- do từ giả thiết ta clig là đường trung
- bình của hình thang ABCD và ra đó DJ
- song song với đường thẳng AB
- như vậy giao tuyến của mặt phẳng SAB và
- YG
- sẽ là đường thẳng đi qua điểm chung nhờ
- vào song song với đường thẳng AB thấy
- gọi nó là đường thẳng d
- như vậy giao tuyến của mặt phẳng s AB và
- AC g là đường thẳng d đi qua G là điểm
- Trung thứ nhất song song với đường thẳng
- a đây
- khi chúng ta sang câu b
- xác định thiết diện tạo bởi hình chóp
- với mặt phẳng p g p bài Toán tiết diện
- thì chúng ta sẽ tìm giao tuyến của mặt
- phẳng Israel với từng mặt phẳng của hình
- chóp SABCD I
- cho đến nay chúng ta để ý ở cô ba chúng
- ta đã xây dựng giao tuyến của mặt phẳng
- SAB với mặt phẳng easy thôi nó sẽ được
- thẳng D nên chúng ta sẽ lấy những phần
- em vừa thuộc đường thẳng d và vừa chụp
- hình chóp SABCD
- dụng cụ thể hơn là lấy đoạn thẳng MN à
- anh như vậy cho mặt phẳng SAB ta có
- đường thẳng d cắt đường thẳng a tại điểm
- M đường thẳng d cắt đường thẳng SB tại
- điểm N thiết diện tạo bởi hình chóp với
- mặt phẳng YG đó là tứ giác m ng I
- chị đã có AB so với YG là đường thẳng MN
- ơ tiếp theo là mặt phẳng kanaid ra với
- mặt phẳng Israel tại đường thẳng mới
- tiếp theo là giao tuyến của mặt phẳng
- Israel
- với mặt phẳng ABCD là đường thẳng easy
- và cuối cùng
- giao tuyến ng là giao tuyến của mặt
- phẳng SBC với mặt phẳng eg I
- đi Câu hỏi tiếp theo là thiết diện là
- hình gì thì cụ thể ta dẫn đường thẳng D
- Hay là đường thẳng MN song song với
- đường thẳng AB đi qua
- MN song song với đường thẳng d
- và do đó ta có thiết diện của chúng ta
- là hình thang mnjy do MN song song với
- EZ II
- Ừ
- Tóm lại khi chúng ta học trường hợp xác
- định giao tuyến của 2 mặt phẳng chứa hai
- đường thẳng song song thì các bài toán
- quy về bài toán tìm giao tuyến của 2 mặt
- phẳng hồng như cách làm không đổi
- cụ thể hơn 2 bàn vào đó là Tìm giao điểm
- của đường thẳng D với mặt phẳng P tìm
- thiết diện tạo bởi mặt phẳng P và hình
- chóp
- để tìm giao điểm của đường thẳng D với
- mặt phẳng P thì chúng ta phần tìm đường
- thẳng d phẩy nằm trong p mà đồng phẳng
- với đường thẳng lên
- thì cách tìm thì chúng ta sẽ tìm mặt
- phẳng quy sao cho D nằm trong mặt phẳng
- tôi có tiếp theo chúng ta sẽ tìm giao
- tuyến B phẩy của P và quy vào đây phải
- là chính là từ thẳng đồng phẳng với
- đường thẳng d mà nằm trong mặt phẳng tên
- là tiếp theo chúng ta sẽ tìm giao điểm
- giữa đường thẳng d và đi khỏi đây chính
- là giao điểm của đường thẳng d và mặt
- phẳng p i
- em còn tìm thiết diện của mặt phẳng P
- với hình chóp thì chúng ta sẽ xác định
- giao tuyến của mặt phẳng tay phải các
- mặt của hình chóp và hai bài toán này
- cần Như là không thay đổi cách làm thì
- chúng ta học cái dạng xác định giao
- tuyến của 2 mặt phẳng chứa hai đường
- thẳng song song thì nó sẽ khác nhau của
- bước tìm giao tuyến của 2 mặt phẳng sẽ
- có thêm trường hợp là chúng chứa hai
- đường thẳng song song a
- ở đây chúng ta sẽ quay lại bài toán tìm
- giao tuyến giữa hai mặt phẳng P bài toán
- tìm giao tuyến của hai mặt phẳng phân
- biệt thì bước đầu tiên xe Tìm kiếm xung
- thứ nhất sau thì Bước tiếp theo là chúng
- ta lại chọn ra hai đường thẳng đồng
- phẳng d thuộc P và đi phẩm thuộc quy như
- trên hình
- nếu như đây có đây phải cắt nhau thì ta
- sẽ có điểm chung thứ hai và nối liền
- Trung thống nhất với điểm Trung thứ hai
- là ta sẽ được giao tuyến giữa hai mặt
- phẳng Còn nếu D vào đây phải chăng sau
- thì chúng ta sẽ dựng giao tuyến đi qua
- điểm số thứ nhất và song song với đêm và
- đến phẩm
- như vậy Thấy nó kêu nó đi xong dặm đầu
- tiên của Bà Trưng hay
- chả có cái Chúc các em học tốt nha
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây