Bài học cùng chủ đề
- Tích của một số với một vectơ
- Định nghĩa và tính chất
- Tính chất trung điểm, trọng tâm. Điều kiện để hai vectơ cùng phương
- Phân tích một vectơ theo hai vectơ không cùng phương
- Độ dài biểu thức vectơ. Phân tích vectơ
- Đẳng thức vectơ
- Tìm điểm thỏa mãn đẳng thức vectơ
- Luyện tập tổng hợp
- Bài tập tự luận: Phân tích một vectơ theo hai vectơ không cùng phương, tìm điểm thỏa mãn hệ thức vectơ
- Bài tập tự luận: Chứng minh đẳng thức vectơ. Chứng minh ba điểm thẳng hàng
- Phiếu bài tập: Tích của vectơ với một số
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tự luận: Phân tích một vectơ theo hai vectơ không cùng phương, tìm điểm thỏa mãn hệ thức vectơ SVIP
Gọi $G$ là trọng tâm của tam giác $A B C$. Hāy biểu diễn các vectơ $\overrightarrow{A B} ; \overrightarrow{B C} ; \overrightarrow{G C} ; \overrightarrow{C A}$ theo $\vec{a}=\overrightarrow{G A}, \vec{b}=\overrightarrow{G B}$.
Hướng dẫn giải:
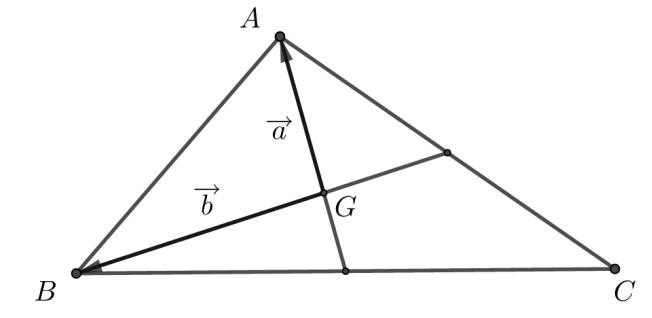
- Ta có: $\overrightarrow{A B}=\overrightarrow{G B}-\overrightarrow{G A}=\vec{b}-\vec{a}$.
- Vì $G$ là trọng tâm của tam giác $A B C$ nên $\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}=\overrightarrow{0} \Rightarrow \overrightarrow{G C}=-\overrightarrow{G A}-\overrightarrow{G B}=-\vec{a}-\vec{b}$.
- Ta có: $\overrightarrow{B C}=\overrightarrow{B G}+\overrightarrow{G C}=-\vec{b}+(-\vec{a}-\vec{b})=-\vec{a}-2 \vec{b}$.
- Ta có: $\overrightarrow{C A}=\overrightarrow{G A}-\overrightarrow{G C}=\vec{a}-(-\vec{a}-\vec{b})=2 \vec{a}+\vec{b}$.
Điểm $M$ gọi là chia đoạn thā̉ng $A B$ theo ti số $k \neq 1$ nếu $M A=k M B$. Chứng minh rā̀ng với mọi điểm $O$ ta có $\overrightarrow{O M}=\dfrac{\overrightarrow{O A}-k \overrightarrow{O B}}{1-k}$.
Hướng dẫn giải:
Từ giả thiết $\overrightarrow{M A}=k \overrightarrow{M B}$, với $k \neq 1$, ta có:
$\begin{aligned}
&\overrightarrow{O A}-\overrightarrow{O M}=k(\overrightarrow{O B}-\overrightarrow{O M}) \Leftrightarrow(1-k) \overrightarrow{O M}=\overrightarrow{O A}-\overrightarrow{O B} . \\
&\Leftrightarrow \overrightarrow{O M}=\frac{\overrightarrow{O A}-k \overrightarrow{O B}}{1-k} .\end{aligned}$
Cho tam giác $A B C$. Gọi $M$ là trung điểm của $A B$ và $N$ là một điểm trên cạnh $A C$ sao cho $N A=2 N C$. Gọi $K$ là trung điểm $M N$. Phân tích vectơ $\overrightarrow{A K}$ theo $\overrightarrow{A B}$ và $\overrightarrow{A C}$.
Hướng dẫn giải:
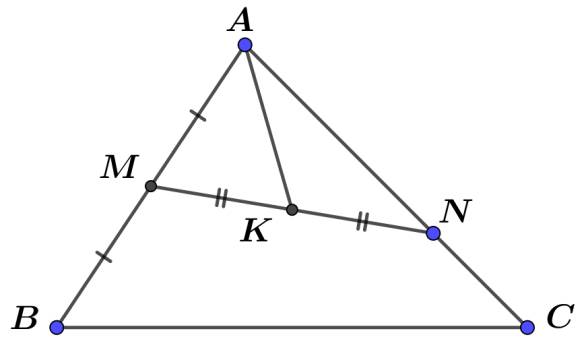
Ta có: $M, K$ lần lượt là trung điểm của $A B, M N$ nên $\overrightarrow{A M}=\dfrac{1}{2} \overrightarrow{A B}$ và $2 \overrightarrow{A K}=\overrightarrow{A M}+\overrightarrow{A N}$.
Mạat khác: $N$ thuộc cạnh $A C$ và $N A=2 N C \Rightarrow \overrightarrow{A N}=\dfrac{2}{3} \overrightarrow{A C}$.
Suy ra $\overrightarrow{A K}=\dfrac{1}{2}(\overrightarrow{A M}+\overrightarrow{A N})=\dfrac{1}{2}\left(\dfrac{1}{2} \overrightarrow{A B}+\dfrac{2}{3} \overrightarrow{A C}\right)=\dfrac{1}{4} \overrightarrow{A B}+\dfrac{1}{3} \overrightarrow{A C}$.
Cho tam giác $A B C$. Gọi $M$ là trung điểm của $A B$ và $N$ là một điểm trên cạnh $A C$ sao cho $N A=2 N C$. Gọi $K$ là trung điểm $M N$. Phân tích vectơ $\overrightarrow{A K}$ theo $\overrightarrow{A B}$ và $\overrightarrow{A C}$.
Hướng dẫn giải:
Ta có: $M, K$ lần lượt là trung điểm của $A B, M N$ nên $\overrightarrow{A M}=\dfrac{1}{2} \overrightarrow{A B}$ và $2 \overrightarrow{A K}=\overrightarrow{A M}+\overrightarrow{A N}$.
Mạat khác: $N$ thuộc cạnh $A C$ và $N A=2 N C \Rightarrow \overrightarrow{A N}=\dfrac{2}{3} \overrightarrow{A C}$.
Suy ra $\overrightarrow{A K}=\dfrac{1}{2}(\overrightarrow{A M}+\overrightarrow{A N})=\dfrac{1}{2}\left(\dfrac{1}{2} \overrightarrow{A B}+\dfrac{2}{3} \overrightarrow{A C}\right)=\dfrac{1}{4} \overrightarrow{A B}+\dfrac{1}{3} \overrightarrow{A C}$.
Hướng dẫn giải:
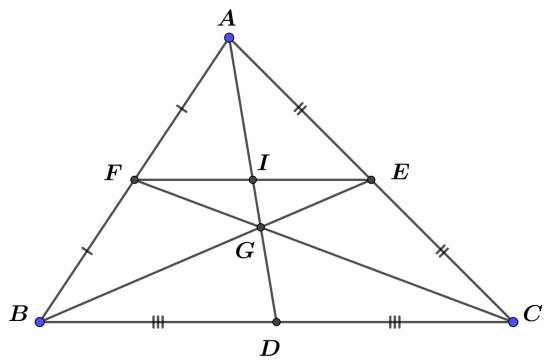
Ta có: $E, F$ lần lượt là trung điểm của $C A, A B \Rightarrow E F$ là đường trung bình của $\triangle A B C \Rightarrow E F / / B C$ $\Rightarrow \dfrac{I E}{C D}=\dfrac{A I}{A D}=\dfrac{I F}{B D} \Rightarrow I F=I E \Rightarrow 2 \overrightarrow{A I}=\overrightarrow{A F}+\overrightarrow{A E} \Rightarrow \overrightarrow{A I}=\dfrac{1}{2}(\vec{u}+\vec{v})$. $G$ là trọng tâm tam giác $A B C ; D, E, F$ lần lượt là trung điểm của $B C, C A A B$ $\Rightarrow \overrightarrow{A G}=\dfrac{2}{3} \overrightarrow{A D}=\dfrac{1}{3}(\overrightarrow{A B}+\overrightarrow{A C})=\dfrac{1}{3}(2 \overrightarrow{A F}+2 \overrightarrow{A E})=\dfrac{2}{3}(\vec{u}+\vec{v}) .$ $D E$ là đường trung bình của $\triangle A B C \Rightarrow D E=\dfrac{1}{2} A B=A F \Rightarrow \overrightarrow{D E}=-\overrightarrow{A F}=-\vec{v}$. $E F$ là đường trung bình của $\triangle A B C \Rightarrow E F=C D \Rightarrow \overrightarrow{D C}=\overrightarrow{F E}=\overrightarrow{A E}-\overrightarrow{A F}=\vec{u}-\vec{v}$.
Cho tam giác $A B C$ có $G$ là trọng tâm.
a) Hāy phân tích véctơ $\overrightarrow{A G}$ theo hai vectơ $\overrightarrow{A B}, \overrightarrow{A C}$.
b) Gọi $E, F$ là hai điểm xác định bởi các điều kiện: $\overrightarrow{E A}=2 \overrightarrow{E B}, 3 \overrightarrow{F A}+2 \overrightarrow{F C}=\overrightarrow{0}$. Hāy phân tích $\overrightarrow{E F}$ theo hai vecto $\overrightarrow{A B}, \overrightarrow{A C}$.
Hướng dẫn giải:
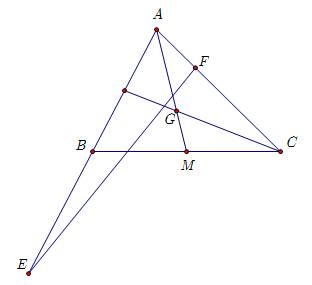
a) Hāy phân tích véctơ $\overrightarrow{A G}$ theo hai vectơ $\overrightarrow{A B}, \overrightarrow{A C}$.
$A G \cap B C=M \Rightarrow M$ là trung điểm $B C \Rightarrow \overrightarrow{A B}+\overrightarrow{A C}=2 \overrightarrow{A M}$.
Mà $G$ là trọng tâm $\triangle A B C \Rightarrow \overrightarrow{A G}=\dfrac{2}{3} \overrightarrow{A M} \Leftrightarrow \overrightarrow{A M}=\dfrac{3}{2} \overrightarrow{A G}$.
$\Rightarrow \overrightarrow{A B}+\overrightarrow{A C}=2 \overrightarrow{A M}=2 \cdot \dfrac{3}{2} \overrightarrow{A G}=3 \overrightarrow{A G} \Rightarrow \overrightarrow{A G}=\dfrac{1}{3} \overrightarrow{A B}+\dfrac{1}{3} \overrightarrow{A C}$
b) Gọi $E, F$ là hai điểm xác định bởi các điều kiện: $\overrightarrow{E A}=2 \overrightarrow{E B}, 3 \overrightarrow{F A}+2 \overrightarrow{F C}=\overrightarrow{0}$. Hāy phân tích $\overrightarrow{E F}$ theo hai vecto $\overrightarrow{A B}, \overrightarrow{A C}$.
Ta có: $\overrightarrow{E F}=\overrightarrow{E A}+\overrightarrow{A F}$.
Theo gt: $\overrightarrow{E A}=2 \overrightarrow{E B} \Rightarrow \overrightarrow{E A}=2 \overrightarrow{A B}$
Từ $3 \overrightarrow{F A}+2 \overrightarrow{F C}=\overrightarrow{0} \Rightarrow \overrightarrow{A F}=\dfrac{2}{5} \overrightarrow{A C}$.
$\Rightarrow \overrightarrow{E F}=\overrightarrow{E A}+\overrightarrow{A F}=2 \overrightarrow{A B}+\dfrac{2}{5} \overrightarrow{A C}$
Cho lục giác đều $A B C D E F$ tâm $O$ cạnh $a$ :
a) Phân tích vectơ $\overrightarrow{A D}$ theo hai véctơ $\overrightarrow{A B}$ và $\overrightarrow{A F}$.
b) Tính độ dài của vecto $\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{B C}$ theo $a$.
Hướng dẫn giải:
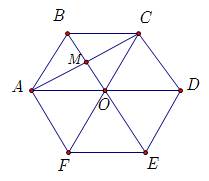
a) Phân tích vectơ $\overrightarrow{A D}$ theo hai vectơ $\overrightarrow{A B}$ và $\overrightarrow{A F}$.
Ta có: $O$ là trung điểm $A D$ nên $\overrightarrow{A D}=2 \overrightarrow{A O}$.
Lại có: $\left\{\begin{array}{l}A B / / F O \\ A F / / B O\end{array} \Rightarrow A B O F\right.$ là hình bình hành $\Rightarrow \overrightarrow{A D}=2 \overrightarrow{A O}=2(\overrightarrow{A B}+\overrightarrow{A F})=2 \overrightarrow{A B}+2 \overrightarrow{A F}$.
b) Tính độ dài của vecto $\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{B C}$ theo $a$.
Ta có: $\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{B C}=\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{B C})=\dfrac{1}{2} \overrightarrow{A C}$.
$$
\Rightarrow\left|\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{B C}\right|=\left|\dfrac{1}{2} \overrightarrow{A C}\right|=\dfrac{1}{2}|\overrightarrow{A C}|=\dfrac{1}{2} A C \text {. }
$$
Theo đề bài: $A B C D E F$ là lục giác đều nên $\triangle A B O ; \triangle C B O$ là tam giác đều cạnh $a$.
Gọi $M$ là trung điểm $B O \Rightarrow A M ; M C$ lần lượt là đường cao $\triangle A B O ; \triangle C B O$ và $A C=A M+M C$ $\Rightarrow A C=A M+M C=\dfrac{a \sqrt{3}}{2}+\dfrac{a \sqrt{3}}{2}=a \sqrt{3} \Rightarrow\left|\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{B C}\right|=\dfrac{1}{2} A C=\dfrac{a \sqrt{3}}{2}$.
Cho hai điểm $A, B$ phân biệt. Xác định điểm $M$ biết $2 \overrightarrow{M A}-3 \overrightarrow{M B}=\overrightarrow{0}$
Hướng dẫn giải:
$ \begin{aligned} &\text { Ta có } 2 \overrightarrow{M A}-3 \overrightarrow{M B}=\overrightarrow{0} \\ &\Leftrightarrow 2 \overrightarrow{M A}-3(\overrightarrow{M A}+\overrightarrow{A B})=\overrightarrow{0} \\ &\Leftrightarrow \overrightarrow{A M}=3 \overrightarrow{A B} \end{aligned} $
$M$ nằm trên tia $AB$ và $A M=3 A B$.
Cho tứ giác $A B C D$. Xác định điểm $M, N, P$ sao cho a) $2 \overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=\overrightarrow{0}$.
b) $\overrightarrow{N A}+\overrightarrow{N B}+\overrightarrow{N C}+\overrightarrow{N D}=\overrightarrow{0}$.
c) $3 \overrightarrow{P A}+\overrightarrow{P B}+\overrightarrow{P C}+\overrightarrow{P D}=\overrightarrow{0}$.
Hướng dẫn giải:
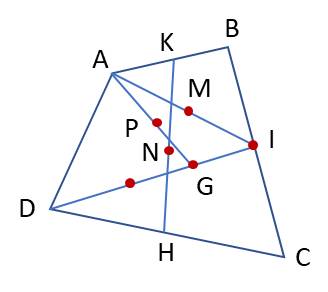
a) Gọi I là trung điểm $\mathrm{BC}$ suy ra $\overrightarrow{M B}+\overrightarrow{M C}=2 \overrightarrow{M I}$
Do đó $2 \overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=\overrightarrow{0}$
$2 \overrightarrow{M A}+2 \overrightarrow{M I}=\overrightarrow{0} \Leftrightarrow \overrightarrow{M A}+\overrightarrow{M I}=\overrightarrow{0}$
Suy ra $M$ là trung điểm $\mathrm{AI}$
b) Gọi $K, H$ lần lượt là trung điểm của $\mathrm{AB}, \mathrm{CD}$ ta có
$\overrightarrow{N A}+\overrightarrow{N B}+\overrightarrow{N C}+\overrightarrow{N D}=\overrightarrow{0} \Leftrightarrow 2 \overrightarrow{N K}+2 \overrightarrow{N H}=\overrightarrow{0}$
$\Leftrightarrow \overrightarrow{N K}+\overrightarrow{N H}=\overrightarrow{0} \Leftrightarrow N$ là trung điểm của $\mathrm{KH}$
c) Gọi $G$ là trọng tâm tam giác $B C D$ khi đó ta có $\overrightarrow{P B}+\overrightarrow{P C}+\overrightarrow{P D}=3 \overrightarrow{P G}$
Suy ra $3 \overrightarrow{P A}+\overrightarrow{P B}+\overrightarrow{P C}+\overrightarrow{P D}=\overrightarrow{0} \Leftrightarrow 3 \overrightarrow{P A}+3 \overrightarrow{P G}=\overrightarrow{0}$
$\Leftrightarrow \overrightarrow{P A}+\overrightarrow{P G}=\overrightarrow{0} \Leftrightarrow P$ là trung điểm $A G$.
Cho trước hai điểm $A, B$ và hai số thực $\alpha, \beta$ thoả mãn $\alpha+\beta \neq 0$. Chứng minh rằng tồn tại duy nhất điểm I thoả mãn $\alpha \overrightarrow{I A}+\beta \overrightarrow{I B}=\overrightarrow{0}$. Từ đó, suy ra với điểm bất kì $M$ thì $\alpha \overrightarrow{M A}+\beta \overrightarrow{M B}=(\alpha+\beta) \overrightarrow{M I}$.
Hướng dẫn giải:
Ta có: $\alpha \overrightarrow{I A}+\beta \overrightarrow{I B}=\overrightarrow{0} \Leftrightarrow \alpha \overrightarrow{I A}+\beta(\overrightarrow{I A}+\overrightarrow{A B})=\overrightarrow{0}$
$$ \Leftrightarrow(\alpha+\beta) \overrightarrow{I A}+\beta \overrightarrow{A B}=\overrightarrow{0} . \Leftrightarrow(\alpha+\beta) \overrightarrow{A I}=\beta \overrightarrow{A B} \Leftrightarrow \overrightarrow{A I}=\dfrac{\beta}{\alpha+\beta} \overrightarrow{A B} $$
Vì A, B cố định nên vectơ $\dfrac{\beta}{\alpha+\beta} \overrightarrow{A B}$ không đổi, do đó tồn tại duy nhất điểm I thoả mãn điều kiện.
Từ đó suy ra
$$ \begin{aligned} &\alpha \overrightarrow{M A}+\beta \overrightarrow{M B}=\alpha(\overrightarrow{M I}+\overrightarrow{I A})+\beta(\overrightarrow{M I}+\overrightarrow{I B}) \\ &=(\alpha+\beta) \overrightarrow{M I}+(\alpha \overrightarrow{I A}+\beta \overrightarrow{I B})=(\alpha+\beta) \overrightarrow{M I}. \end{aligned} $$
