Bài học cùng chủ đề
- Định nghĩa và tính chất
- Tính chất trung điểm, trọng tâm. Điều kiện để hai vectơ cùng phương
- Phân tích một vectơ theo hai vectơ không cùng phương
- Độ dài biểu thức vectơ. Phân tích vectơ
- Đẳng thức vectơ
- Tìm điểm thỏa mãn đẳng thức vectơ
- Luyện tập tổng hợp
- Bài tập tự luận: Phân tích một vectơ theo hai vectơ không cùng phương, tìm điểm thỏa mãn hệ thức vectơ
- Bài tập tự luận: Chứng minh đẳng thức vectơ. Chứng minh ba điểm thẳng hàng
- Phiếu bài tập: Tích của vectơ với một số
- Tích của một số với một vectơ
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tích của một số với một vectơ SVIP
Nội dung này do giáo viên tự biên soạn.
1. Tích của một số với một vectơ và tính chất
Cho số thực \(k\) và vectơ \(\overrightarrow{a}\) khác \(\overrightarrow{0}\). Tích của số \(k\) với vectơ \(\overrightarrow{a}\) là một vectơ, kí hiệu là \(k\overrightarrow{a}\).
Vectơ \(k\overrightarrow{a}\) cùng hướng với vectơ \(\overrightarrow{a}\) nếu \(k>0\), ngược hướng với vectơ \(\overrightarrow{a}\) nếu \(k< 0\) và có độ dài bằng \(\left|k\right|\left|\overrightarrow{a}\right|\).
Quy ước \(0\overrightarrow{a}=\overrightarrow{0},k\overrightarrow{0}=\overrightarrow{0}.\)
Tính chất
Với hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) bất kì, với mọi số thực \(h,k\), ta có:
- \(k\left(\overrightarrow{a}+\overrightarrow{b}\right)=k\overrightarrow{a}+k\overrightarrow{b};\)
- \(\left(h+k\right)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a};\)
- \(h\left(k\overrightarrow{a}\right)=\left(hk\right)\overrightarrow{a};\)
- \(1\overrightarrow{a}=\overrightarrow{a};\left(-1\right)\overrightarrow{a}=-\overrightarrow{a}.\)
2. Điều kiện để hai vectơ cùng phương
Hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\left(\overrightarrow{b}\ne\overrightarrow{0}\right)\) cùng phương khi và chỉ khi có số \(k\) để \(\overrightarrow{a}=k\overrightarrow{b}.\)
Nhận xét: Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi có số thực \(k\) khác \(0\) để \(\overrightarrow{AB}=k\overrightarrow{AC}\).
Chú ý: Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) không cùng phương. Với mọi vectơ \(\overrightarrow{c}\) có duy nhất cặp số \(\left(m;n\right)\) thỏa mãn \(\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}.\)
Ví dụ: Cho tam giác \(ABC\), điểm \(M\) trên cạnh \(BC\) sao cho \(MB=2MC\). Hãy phân tích vectơ \(\overrightarrow{AM}\) theo hai vectơ \(\overrightarrow{u}=\overrightarrow{AB}\) và \(\overrightarrow{v}=\overrightarrow{AC.}\)
Giải
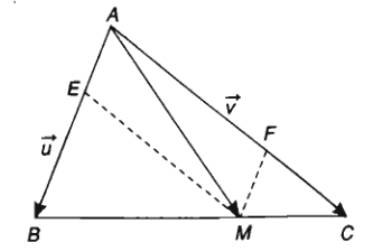
Ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}.\)
\(=\dfrac{1}{3}\overrightarrow{u}+\dfrac{2}{3}\overrightarrow{v}.\)

Bạn có thể đánh giá bài học này ở đây