cho 3 số thực dương thỏa mãn \(\frac{1}{a}+\frac{2}{b}+\frac{3}{c}=3\).Chứng minh rằng
\(\frac{27a^2}{c\left(c^2+9a^2\right)}+\frac{b^2}{a\left(4a^2+b^2\right)}+\frac{8c^2}{b\left(9b^2+4c^2\right)}\ge\frac{3}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 10 2017
Đặt \(\frac{1}{a}=x\); \(\frac{2}{b}=y;\frac{3}{c}=z\)
=>VT = \(\frac{z^3}{x^2+z^2}+\frac{x^3}{y^2+x^2}+\frac{y^3}{y^2+z^2}\)
Ta có \(\frac{z^3}{x^2+z^2}=z-\frac{x^2z}{x^2+z^2}\ge z-\frac{x^2z}{2xz}=z-\frac{x}{2}\)
CMTT:
=> VT \(\ge\frac{x+y+z}{2}=\frac{3}{2}\). Dấu = khi a=1; b=2; z=3
TN
4 tháng 9 2016
Bạn có thể tham khảo cách này
Đặt \(\hept{\begin{cases}\frac{1}{a}=x\\\frac{2}{b}=y\\\frac{3}{c}=z\end{cases}}\Rightarrow x+y+z=3\)
BĐT thành \(\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{3}{2}\left(1\right)\)
ta sẽ dùng Bđt Cói \(\frac{x^3}{x^2+y^2}=x-\frac{xy^2}{x^2+y^2}\ge x-\frac{xy^2}{2xy}=x-\frac{y}{2}\)
Tương tự rồi cộng lại
\(\left(1\right)\ge x+y+z-\frac{x+y+z}{2}=3-\frac{3}{2}=\frac{3}{2}\)
Dấu = khi \(x=y=z=1\Rightarrow\hept{\begin{cases}a=1\\b=2\\c=3\end{cases}}\)
TN
4 tháng 9 2016
Đặt \(\hept{\begin{cases}x=\frac{1}{a}\\y=\frac{2}{b}\\z=\frac{3}{c}\end{cases}\Rightarrow}\hept{\begin{cases}x,y,z>0\\x+y+z=3\end{cases}}\)
Khi đó ta có BĐT cần chứng minh tương đương với:
\(P=\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{3}{2}\)
Ta có: \(P\ge\frac{\left(x^2+y^2+z^2\right)^2}{x^2y+y^2z+z^2x+xy^2+yz^2+zx^2}\)
Ta cũng có: \(3\left(x^2+y^2+z^2\right)=\left(x+y+z\right)\left(x^2+y^2+z^2\right)\)
\(=x^3+y^3+z^3+xy^2+yz^2+zx^2+x^2y+y^2z+z^2x\)
\(\ge3\left(x^2y+y^2z+z^2x\right)\)
\(\Rightarrow x^2y+y^2z+z^2x\le x^2+y^2+z^2\)
Chứng minh tương tự ta có: \(xy^2+yz^2+zx^2\le x^2+y^2+z^2\)
\(\Rightarrow P\ge\frac{x^2+y^2+z^2}{2}\ge\frac{\left(x+y+z\right)^2}{3}=\frac{3}{2}\)
Dấu = khi \(x=y=z\)hay\(\hept{\begin{cases}a=1\\b=2\\b=3\end{cases}}\)
TN
16 tháng 1 2018
Thôi làm luôn ( ͡° ͜ʖ ͡°)
\(\left(\frac{1}{a};\frac{2}{b};\frac{3}{c}\right)\rightarrow\left(x;y;z\right)\Rightarrow\hept{\begin{cases}x+y+z=3\\x,y,z>0\end{cases}}\)
Và \(BDT\Leftrightarrow\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{x^2+z^2}\ge\frac{3}{2}\)
Áp dụng BĐT AM-GM ta có:
\(\frac{x^3}{x^2+y^2}=x-\frac{xy^2}{x^2+y^2}\ge x-\frac{xy^2}{2xy}=x-\frac{y}{2}\)
Tương tự cho 2 BĐT còn lại rồi cộng theo vế:
\(VT\ge x+y+z-\frac{x+y+z}{2}=3-\frac{3}{2}=\frac{3}{2}\)
\("="\Leftrightarrow x=y=z=1\Leftrightarrow a=1;b=2;c=3\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2019
\(\left(a+\frac{4b}{c^2}\right)\left(b+\frac{4c}{a^2}\right)\left(c+\frac{4a}{b^2}\right)\ge2\sqrt{\frac{4ab}{c^2}}.2\sqrt{\frac{4bc}{a^2}}.2\sqrt{\frac{4ac}{b^2}}=64\)
Dấu "=" xảy ra khi \(a=b=c=2\)
\(\frac{a^3}{b}+ab\ge2a^2\) ; \(\frac{b^3}{c}+bc\ge2b^2\); \(\frac{c^3}{a}+ac\ge2c^2\)
\(\Rightarrow\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge2\left(a^2+b^2+c^2\right)-\left(ab+bc+ca\right)\ge2\left(ab+bc+ca\right)-\left(ab+bc+ca\right)=ab+bc+ca\)
Dấu "=" xảy ra khi \(a=b=c\)
VD
27 tháng 4 2020
\(=\)\(18\left(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}\right)\)\(=\)\(18\frac{3}{1}\)\(>\)\(\left(9+5\sqrt{3}\right)\left(a^2+b^2+c^2\right)\)\(=\)\(0\)
Vậy\(18\frac{3}{1}\)\(>\)\(0\)
Chứng minh là \(18\frac{3}{1}\)\(>\)\(0\)là đúng
chúc bạn học tốt
A
27 tháng 4 2020
Bất đẳng thức trên
<=> 
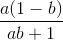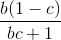+ 1 + 
+ 1 +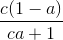 
+ 1 ≥ 3
<=> 
+ 
+ 
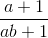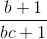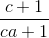≥ 3 (*)
Ta có: VT(*) ≥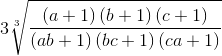 
Ta sẽ chứng minh: (a + 1)(b + 1)(c + 1) ≥ (ab + 1)(bc + 1)(ca + 1)
<=> abc + ab + bc + ca + a + b + c + 1
≥ a2b2c2 + abc(a + b + c) + ab + bc + ca + 1
<=> 3 ≥ a2b2c2 + 2abc (**)
Theo Cosi: 3 = a + b + c ≥ 3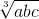
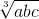=> ≤ 1 => abc ≤ 1
Vậy (**) đúng => (*) đúng.
Đặt \(a=\frac{1}{x};b=\frac{2}{y};c=\frac{3}{z}\)
Theo bài ra, ta có:
x+y+z=3
\(bđt\Leftrightarrow\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{3}{2}\)
Áp dụng kĩ thuật Cau-chy ngược dấu ta có:
\(\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{x+y+z}{2}=\frac{3}{2}\)
Dấu '=' xảy ra <=> a=3;b=2;c=1
*Bài khá giống bạn kia :)
Đặt \(a=\frac{1}{x};b=\frac{2}{y};c=\frac{3}{z}\)
\(\Rightarrow x+y+z=3\)
BĐT cần chứng minh trở thành :
\(\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{3}{2}\)
Áp dụng kĩ thuật Cô Si ngược dấu ta có :
\(\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{x+y+z}{2}=\frac{3}{2}\)
Dấu đẳng thức xảy ra \(\Leftrightarrow a=3;b=2;c=1\)