Cho tam giác ABC,góc B=120 độ,AB=6cm,AC=14cm
Tính độ dài cạnh BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



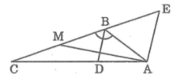

Suy ra tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
![]()


Theo bất đẳng thức tam giác, ta có:
\(AB+BC>AC< AB-BC\)
\(\Rightarrow6+4>AC< 6-4\)
\(\Rightarrow10>AC< 2\)
.....
Còn dữ liệu B = 60 độ em ko bt lm sao để giải AC chính xác, dù j e cx chỉ ms lớp 7 nên lm đc cách này thôi

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-6^2=64\)
hay AC=8(cm)
Vậy: AC=8cm
b) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)

75%=3/4
Tổng dộ dài AB và AC là:3+4=7(phần)
Gía trị 1 phần là :120:(3+4+5)=10(cm)
AC=10 x 3=30(cm)
AB=10 x 4=40(cm)
BC=10 x 5=50(cm)
Diện tích tam giác ABC là: (30 x 40):2=60(cm2)
Chiều cao tương ứng của cạnh BC là: 60 x 2:5=24(cm)
Ta có : AB2 +BC2=AC2 (đ/lí pi-ta-go)
62+BC2=142
BC2=142-62
BC2=196-36
BC2=160
=) BC2=√160