Cho tam giác ABC, trọng tâm G(AB<AC). Qua G vẽ đường thẳng d cắt các cạnh AB,AC ở D và E. Chứng minh rằng
\(\frac{AB}{AD}+\frac{AC}{AE}=3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 7 2023
Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm
DT
20 tháng 4 2022
Hình em tự vẽ ra nhé.
Áp dụng đl pytago vào tam giác vuông ABC có:
AB^2 + AC^2 = BC^2
-- > BC = 5 (cm)
Vì tam giác ABC vuông tại A, AM là đường trung tuyến ứng với cạnh huyền BC nên ta có:
\(AM=\dfrac{1}{2}BC=\dfrac{1}{2}.5=2,5\left(cm\right)\)
Vì G là trọng tâm tâm giác ABC, ta lại có:
\(AG=\dfrac{2}{3}AM=\dfrac{2}{3}.2,5=\dfrac{5}{3}\left(cm\right)\)
CM
13 tháng 6 2018
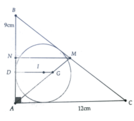
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm
CM
28 tháng 4 2019
Vì tam giác ABC cân tại A nên đường trung trực của cạnh đáy BC đồng thời là trung tuyến của tam giác ABC ứng với cạnh BC.
Kết hợp với giả thiết suy ra G là trọng tâm của tam giác ABC.
NN
2
KN
26 tháng 2 2020
Gọi trung tuyến ứng với cạnh BC là AM
Giả sử AB < AC
Xét \(\Delta\)AMB và \(\Delta\)AMC có
AM: cạnh chung
BM = CM (gt)
AB < AC (điều giả sử)
Do đó ^AMB < ^AMC
Tiếp tục xét \(\Delta\)GMB và \(\Delta\)GMC có:
GM: cạnh chung
BM = MC (gt)
^AMB < ^AMC (cmt)
Do đó BG < CG
Kết hợp với AB < AC (gt) suy ra AB + BG < AC + CG (trái với gt)
Tương tự AB > AC cũng là điều sai
Vậy AB = AC hay \(\Delta\)ABC cân tại A (đpcm)
I
26 tháng 2 2020
Gọi trung tuyến ứng với cạnh BC là AM
Giả sử AB < AC
Xét ΔAMB và ΔAMC có
AM: cạnh chung
BM = CM (gt)
AB < AC (điều giả sử)
Do đó ^AMB < ^AMC
Tiếp tục xét ΔGMB và ΔGMC có:
GM: cạnh chung
BM = MC (gt)
^AMB < ^AMC (cmt)
Do đó BG < CG
Kết hợp với AB < AC (gt) suy ra AB + BG < AC + CG (trái với gt)
Tương tự AB > AC cũng là điều sai
Vậy AB = AC hay ΔABC cân tại A (đpcm)
CM
7 tháng 4 2019
Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F ⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B
Gia sử AB < AC
Vẽ BM , CN // DE , vẽ trung tuyến AF => A;F;G thẳng hàng ; AF = 3/2 AG
Tam giác BMF = tam giác CNF ( g.c.g )
=> MF = NF
Có : BM , CN // DE
=> AB/AD = AM/AG ; AC/AE = AN/AG
=> AB/AD + AC/AE = AM+AN/AG = AF-MF+AF+NF/AG = 2AF/AG = 3
P/S : tham khảo