Bài 1. Cho tam giác ABC vuông tại A, đường cao AH. các đường tròn đường kính BH và đường kính CH cắt AB, AC theo thứ tự tại D, E. chứng mình rằng:a) AD.AB = AE,ACb) Đường thẳng DE là tiếp tuyến chung của 2 đường tròn đã cho.Bài 2. Chứng minh rằng: với mọi x,y,z \(\in\)R ta có\(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\)Bài 3. Cho biểu...
Đọc tiếp
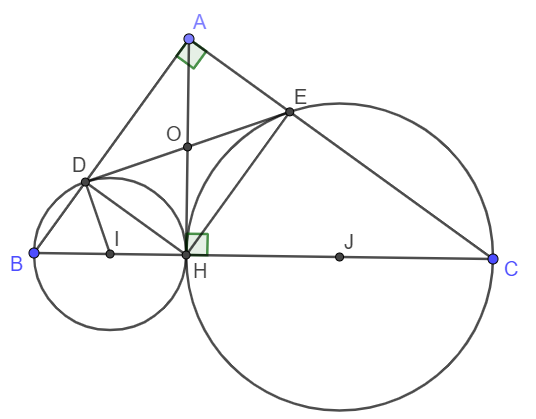
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH. các đường tròn đường kính BH và đường kính CH cắt AB, AC theo thứ tự tại D, E. chứng mình rằng:
a) AD.AB = AE,AC
b) Đường thẳng DE là tiếp tuyến chung của 2 đường tròn đã cho.
Bài 2. Chứng minh rằng: với mọi x,y,z \(\in\)R ta có
\(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\)
Bài 3. Cho biểu thức: \(P=\frac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\frac{2x+\sqrt{x}}{\sqrt{x}}+\frac{2\left(x-1\right)}{\sqrt{x}-1}\)
a) Rút gọn P
b) Tìm GTNN của P
Mk làm cho bài bđt nha
Bài 2 :
Có : (x-y)^2 >= 0
<=> x^2-2xy+y^2 >= 0
<=> x^2+y^2 >= 2xy
Tương tự : y^2+z^2 >= 2yz ; z^2+x^2 >= 2zx
=> 2.(x^2+y^2+z^2) >= 2xy+2yz+2zx
<=> x^2+y^2+z^2 >= xy+yz+zx
<=> x^2+y^2+z^2+2xy+2yz+2zx >= 3.(xy+yz+zx)
<=> (x+y+z)^2 >= 3.(xy+yz+zx)
=> ĐPCM
Dấu "=" xảy ra <=> x=y=z
Tk mk nha