Cho biểu thức:
A=(6x−x2x+1+10x2−1).x+12−5xx−1(6x−x2x+1+10x2−1).x+12−5xx−1
a)Rút gọn A
b)chứng minh:với mọi x=±±1 thì A luôn có giá trị âm
c)tìm GTLN của A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x ≠ 0 , x ≠ − 2
b) Ta có D = x 2 - 2x - 2.
c) Chú ý D = - x 2 - 2x - 2 = - ( x + 1 ) 2 - 1 ≤ -1. Từ đó tìm được giá trị lớn nhất của D = -1 khi x = -1.

Điều kiện x ≠ -2 và x ≠ 0
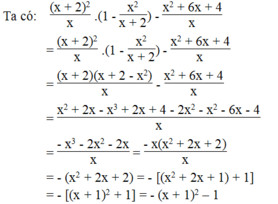
Vì x + 1 2 ≥ 0 nên - x + 1 2 ≤ 0 ⇒ - x + 1 2 - 1 ≤ - 1
Khi đó biểu thức có giá trị lớn nhất bằng -1 khi x = -1
Vậy biểu thức đã cho có giá trị lớn nhất bằng -1 tại x = -1.

\(a,ĐK:x\ne2\\ b,A=\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3}{x-2}\\ c,x=\dfrac{2021}{1010}\Leftrightarrow A=\dfrac{3}{\dfrac{2021}{1010}-\dfrac{2020}{1010}}=\dfrac{3}{\dfrac{1}{1010}}=3030\)

a) rút gọn ta được \(A=\dfrac{-x^2+6x-10}{2}\)
b) ta thấy tử phân tích thành \(-\left(x-3\right)^2-1\le-1< 0\)
-> A <0
c)vì tử luôn \(\le\)1-> \(A\le-\dfrac{1}{2}\)dấu bằng sảy ra khi x=3

a: \(A=\dfrac{3\left(1-2x\right)}{2x\left(x^2+1\right)-\left(x^2+1\right)}\)
\(=\dfrac{-3\left(2x-1\right)}{\left(x^2+1\right)\left(2x-1\right)}=\dfrac{-3}{x^2+1}\)
b: Khi x=3 thì \(A=\dfrac{-3}{3^2+1}=-\dfrac{3}{10}\)
c: x^2+1>=0
=>3/x^2+1>=0
=>-3/x^2+1<=0
=>A<=0(ĐPCM)

`a)` Thay `x=2` vào `B` có: `B=[-10]/[2-4]=5`
`b)` Với `x ne -1;x ne -5` có:
`A=[(x+2)(x+1)-5x-1-(x+5)]/[(x+1)(x+5)]`
`A=[x^2+x+2x+2-5x-1-x-5]/[(x+1)(x+5)]`
`A=[x^2-3x-4]/[(x+1)(x+5)]`
`A=[(x+1)(x-4)]/[(x+1)(x+5)]`
`A=[x-4]/[x+5]`
`c)` Với `x ne -5; x ne -1; x ne 4` có:
`P=A.B=[x-4]/[x+5].[-10]/[x-4]`
`=[-10]/[x+5]`
Để `P` nguyên `<=>[-10]/[x+5] in ZZ`
`=>x+5 in Ư_{-10}`
Mà `Ư_{-10}={+-1;+-2;+-5;+-10}`
`=>x={-4;-6;-3;-7;0;-10;5;-15}` (t/m đk)

\(A=x^2-6x+10\)
\(=x^2-6x+9+1\)
\(=\left(x-3\right)^2+1\)
\(\left(x-3\right)^2\ge0\)
\(\Rightarrow\left(x-3\right)^2+1\ge1>0\)
Vậy A > 0 với mọi x.
\(B=x^2-2xy+y^2+1\)
\(=\left(x-y\right)^2+1\)
\(\left(x-y\right)^2\ge0\)
\(\Rightarrow\left(x-y\right)^2+1\ge1>0\)
Vậy B > 0 với mọi x, y.
\(M=x^2-6x+12\)
\(=x^2-6x+9+3\)
\(=\left(x-3\right)^2+3\)
\(\left(x-3\right)^2\ge0\)
\(\Rightarrow\left(x-3\right)^2+3\ge3\)
\(MinB=3\Leftrightarrow x=3\)
\(\left(x+3\right)^2+\left(x-2\right)\left(x+2\right)-2\left(x-1\right)^2=7\)
\(x^2+6x+9+x^2-4-2\left(x^2-2x+1\right)=7\)
\(2x^2+6x+5-2x^2+4x-2=7\)
\(10x=7+3\)
\(10x=10\)
\(x=1\)
\(x^2+x=0\)
\(x\left(x+1\right)=0\)
\(\left[\begin{array}{nghiempt}x=0\\x+1=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=0\\x=-1\end{array}\right.\)
\(x^3-\frac{1}{4}x=0\)
\(x\left(x^2-\frac{1}{4}\right)=0\)
\(x\left(x-\frac{1}{2}\right)\left(x+\frac{1}{2}\right)=0\)
\(\left[\begin{array}{nghiempt}x=0\\x-\frac{1}{2}=0\\x+\frac{1}{2}=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=0\\x=\frac{1}{2}\\x=-\frac{1}{2}\end{array}\right.\)
\(\left(x+10\right)^2-\left(x^2+2x\right)\)
\(=x^2+20x+100-x^2-2x\)
\(=18x+100\)
\(\left(x+2\right)\left(x-2\right)+\left(x-1\right)\left(x^2+x+1\right)-x\left(x^2+x\right)\)
\(=x^2-4+x^3-1-x^3-x^2\)
\(=-5\)
hello
a)A=1(6x-x2x+1+10x2-1)x-1(6x-x2x+1+10x2-1)x+12-5xx-5xx+12-1
A=\(14-10x^2-1\)
b)thay 1 vao A ta có
\(A=14-10.1^2-1=14-10-1=13\)
thay -1 vào A ta có
\(A=14-10\left(-1\right)^2-1=14+10-1=23\)
vậy với x=+-1 thì x luôn dương
c)