Bài 37 : Tìm giá trị của biểu thức sau 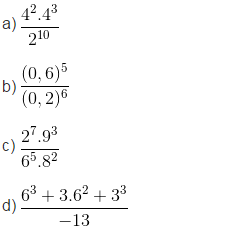
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: \(x^2+5x=x\left(x+5\right)\)
Để biểu thức này âm thì \(x\left(x+5\right)< 0\)
hay -5<x<0
b: \(3\left(2x+3\right)\left(3x-5\right)< 0\)
\(\Leftrightarrow-\dfrac{3}{2}< x< \dfrac{5}{3}\)

P= (x2+2xy+y2)+(x+y)+(x2+4x+4)+21/4
P=(x+y)2+2(x+y)x1/2+1/4+(x+2)2+5
p=(X+Y+1/2)2+(x+2)2+5 >=0
Dấu bằng xảy ra khi:
x+y+1/2=0
x+2=0
Bạn tự giải nốt nhé
bạn ơi giải thích cho mình tại sao lại lấy được P=(x+y+1/2)^2 + (x+2)^2+5 đc ko

Bài 1:
Ta có |x-8| > 0 với mọi x
=>A=37-|x-8| > 37 với mọi x
Vậy GTLN của A=37 với x-8=0 =>x=8
Bài 2 tương tự nhé
Học tốt :))

mik giải theo cái 37-3x/10-x nha Azure phan bảo linh
cái pải z ko bn
bài toán :
\(\frac{37-3x}{10}-x\)
Rút gọn biểu thức:
\(\frac{-\left(13x-37\right)}{10}\)
Hoặc là : Phân tích thành nhân tử
\(\frac{18\frac{1}{2}-\frac{13x}{2}}{5}\)\(nha\)

23 + 39 + 37 + 21 + 34 + 26
= (23 + 37) + (39 + 21) + (34 + 26)
= 60 + 60 + 60
= 60 x 3
= 180
23 + 39 + 37 + 21 + 34 + 26
=(23 + 37) + (39 + 21) + (34 + 26)
=60 + 60 + 60
=60 × 3
=180

Bài 1:
a) \(x^2+5x=x\left(x+5\right)< 0\) (1)
Nhận thấy: \(x< x+5\)
nên từ (1) \(\Rightarrow\) \(\hept{\begin{cases}x< 0\\x+5>0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x< 0\\x>-5\end{cases}}\)\(\Leftrightarrow\)\(-5< x< 0\)
Vậy.....
b) \(3\left(2x+3\right)\left(3x-5\right)< 0\)
TH1: \(\hept{\begin{cases}2x+3>0\\3x-5< 0\end{cases}}\)\(\Leftrightarrow\) \(\hept{\begin{cases}x>-\frac{3}{2}\\x< \frac{5}{3}\end{cases}}\)\(\Leftrightarrow\)\(-\frac{3}{2}< x< \frac{5}{3}\)
TH2: \(\hept{\begin{cases}2x+3< 0\\3x-5>0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x< -\frac{3}{2}\\x>\frac{5}{3}\end{cases}}\) vô lí
Vậy \(-\frac{3}{2}< x< \frac{5}{3}\)
Bài 2:
a) \(2y^2-4y=2y\left(y-2\right)>0\)
TH1: \(\hept{\begin{cases}y>0\\y-2>0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}y>0\\y>2\end{cases}}\)\(\Leftrightarrow\)\(y>2\)
TH2: \(\hept{\begin{cases}y< 0\\y-2< 0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}y< 0\\y< 2\end{cases}}\)\(\Leftrightarrow\)\(y< 0\)
Vậy \(\orbr{\begin{cases}y< 0\\y>2\end{cases}}\)
b) \(5\left(3y+1\right)\left(4y-3\right)>0\)
TH1: \(\hept{\begin{cases}3y+1>0\\4y-3>0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}y>-\frac{1}{3}\\y>\frac{3}{4}\end{cases}}\)\(\Leftrightarrow\)\(y>\frac{3}{4}\)
TH2: \(\hept{\begin{cases}3y+1< 0\\4y-3< 0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}y< -\frac{1}{3}\\y< \frac{3}{4}\end{cases}}\)\(\Leftrightarrow\)\(y< -\frac{1}{3}\)
Vậy \(\orbr{\begin{cases}y>\frac{3}{4}\\y< -\frac{1}{3}\end{cases}}\)
a)\(\dfrac{4^2.4^3}{2^{10}}=\dfrac{\left(2^2\right)^2.\left(2^2\right)^3}{2^{10}}=\dfrac{2^4.2^6}{2^{10}}=1\)
b)\(\dfrac{\left(0,6\right)^5}{\left(0,2\right)^6}=\dfrac{\left(0,2\right)^5.3^5}{\left(0,2\right)^5.0,2}=\dfrac{3^5}{0,2}=1215\)
c)\(\dfrac{2^7.9^3}{6^5.8^2}=\dfrac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\dfrac{2^7.3^6}{2^5.3^5.2^6}=\dfrac{3}{2^4}=\dfrac{3}{16}\)
d)\(\dfrac{6^3+3.6^2+3^3}{-13}\)=\(\dfrac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\dfrac{3^3.\left(2^3+2^2+1\right)}{-13}=\dfrac{3^3.13}{-13}=-3^3=-27\)
a) 1
b) 1215
c) 0,1875
d) -27