Cho \(\Delta ABC\) có AD là phân giác \(\widehat{BAC}\)( D \(\in BC\)) Từ D kẻ các đường thẳng song song với AB, AC cắt AC, AB lần lượt tại E và F. a) CM: Tứ giác AEDF là hình thoi.b) Trên tia AB lấy G sao cho F là trung điểm AG. CM: tứ giác EFGD là hình bình hành.c) Gọi I là điểm đối xứng của D qua F, tia IA cắt tia DE tại K. Gọi O là giao điểm của AD và EF. CM: G đối xứng với K qua O.d) Tìm điều...
Đọc tiếp
Cho \(\Delta ABC\) có AD là phân giác \(\widehat{BAC}\)( D \(\in BC\)) Từ D kẻ các đường thẳng song song với AB, AC cắt AC, AB lần lượt tại E và F.
a) CM: Tứ giác AEDF là hình thoi.
b) Trên tia AB lấy G sao cho F là trung điểm AG. CM: tứ giác EFGD là hình bình hành.
c) Gọi I là điểm đối xứng của D qua F, tia IA cắt tia DE tại K. Gọi O là giao điểm của AD và EF. CM: G đối xứng với K qua O.
d) Tìm điều kiện của \(\Delta ABC\)để tứ giác ADGI là hình vuông.
Câu a) và b) mk lm đc rùi.
NHỜ MỌI NGƯỜI CÂU C) VÀ CÂU D)
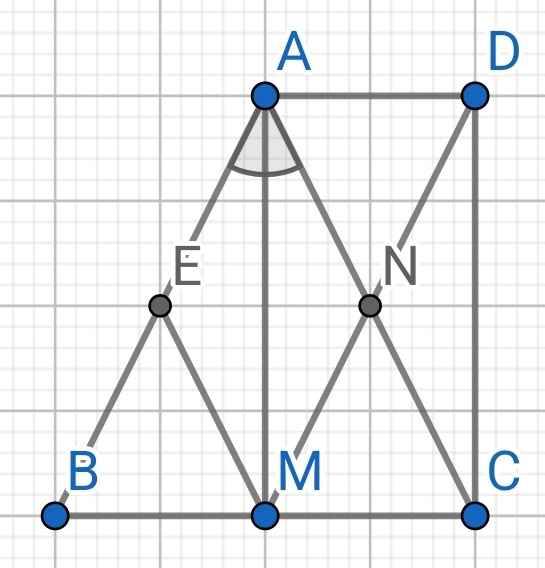
Hình bạn tự vẽ nhé!
c) Bạn có: EFGD là hình bình hành
=> FG // ED
FG = ED
Mà FG = FA ; ED = EK
=> AG // DK
AG = DK
=> AGDK là hình bình hành
Lại có O là trung điểm AD
=> O là trung điểm GK
=> G đối xứng K qua O
d) Mình làm tắt:
Để AIGD là hình vuông thì
\(\hept{\begin{cases}AD\perp GD\\AD=GD\end{cases}}\)
\(\Rightarrow\Delta ABC\)vuông cân