Cho đường thẳng \(xx'\) , một điểm O nằm trên đường thẳng ấy . Trên hai nửa mặt phẳng đối nhau bờ là đường thẳng \(xx'\) , lấy hai điểm \(A,B\) Sao cho \(\widehat{x'OA}=150^o\) và \(\widehat{BOx}=30^o\) . Chứng tỏ tia \(Ox\) là tia phân giác của góc \(\widehat{AOB}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B x x' 30 150 O
Ta có: \(\widehat{xOA}+\widehat{x'OA}=180^o\)
\(\Rightarrow\widehat{xOA} +150^o=180^o\)
\(\Rightarrow\widehat{xOA}=180^o-150^o=30^o\)
mà \(\widehat{xOB}=30^o\)
\(\Rightarrow\widehat{xOA}=\widehat{xOB}\left(=30^o\right)\)
=> Ox là tia phân giác của góc AOB

ta có \(\widehat{xOy}+\widehat{x'Oy}=180^o\)(2 góc kề bù)
Hay \(\widehat{xOy}\)+120o=180o
=> \(\widehat{xOy}\)=60o
s2 ta thấy \(\widehat{xOy}>\widehat{xOz}\)(60o>40o)
=> Oz nằm giữa Ox và Oy
b,do Oz là pg của góc xOy => \(\widehat{z'Oy}=\widehat{z'Ox'}=\frac{1}{2}\widehat{x'Oy}=60^o\)
Ta có \(\widehat{xoz}+\widehat{zOy}=\widehat{xOy}=60^o\)
=>\(\widehat{zOy}=20^o\)
s2 ta được \(\widehat{zOy}< \widehat{yOz}\)(20o<60o)
=>Oy nằm giữa Oz và Oz'
=>\(\widehat{zOy}+\widehat{yOz'}=\widehat{zOz'}\)
Hay 20o+60o=\(\widehat{zoz'}\)
=> \(\widehat{zOz'}=80^o\)
tk mk nhé

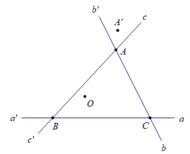
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.

\(\widehat{xAM}\) và \(\widehat{MAy}\) kể bù \(\Rightarrow\widehat{MAy}=60^o\)
Tương tự \(\widehat{yAN}=60^o\)
Mà AM, AN nằm giữa ở 2 nửa mặt phẳng đối nhau bờ Ay
\(\Rightarrow Ay\) nằm giữa AM và AN
\(\Rightarrow\widehat{MAN}=\widehat{MAy}+\widehat{yAN}=120^o\)
ˆxAMxAM^ và ˆMAyMAy^ kể bù ⇒ˆMAy=60o⇒MAy^=60o
Tương tự ˆyAN=60oyAN^=60o
Mà AM, AN nằm giữa ở 2 nửa mặt phẳng đối nhau bờ Ay
⇒Ay⇒Ay nằm giữa AM và AN
⇒ˆMAN=ˆMAy+ˆyAN=120o