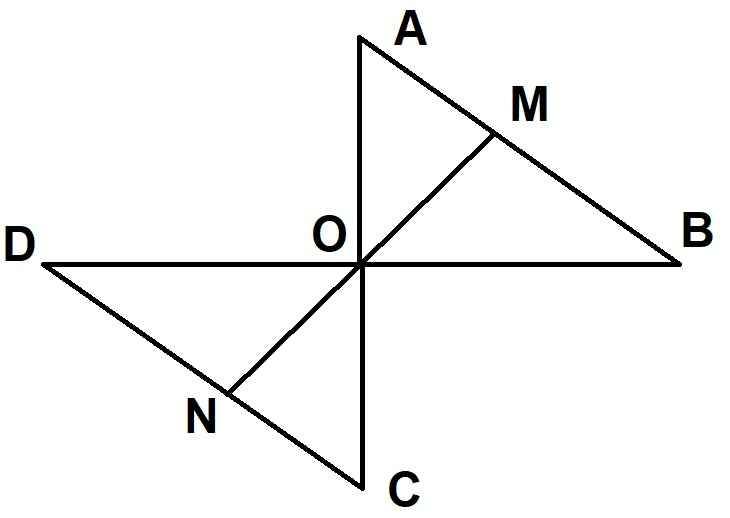
Cho tam giác AOB.trên tia đối của OA lấy điểm C sao cho OA=OC.trên tia đối của OB lấy điểm D sao cho OB=OD
1.chứng minh tam giác AOB= tam giác COD
2. gọi M là điểm giữa A và B.Tia MO cắt CD tại N.chứng minh MB=ND
3.chứng minh BC//AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)

b: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD

a: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD

b: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD

a) xét \(\Delta DOC,\Delta BOA:\)
\(\widehat{DOC}=\widehat{BOA}\left(đđ\right)\)
OA = OC ( gt )
OD = OB ( gt )
\(\rightarrow\Delta DOC=\Delta BOA\left(c.g.c\right)\)
\(\Rightarrow\widehat{ODC}=\widehat{OBA}\) ( 2 góc tương ứng )
mà chúng lại nằm ở vị trí so le trong
\(\Rightarrow\) AB// CD
c) xét \(\Delta IOM,\Delta FON:\)
ON = OM ( \(\Delta AOM=\Delta CON\) )
\(\widehat{O_1}=\widehat{O_2}\) ( đđ)
\(\widehat{I}=\widehat{F}=90^o\left(gt\right)\)
\(\rightarrow\Delta IOM=\Delta FON\) ( cạnh huyền góc nhọn )
\(\Rightarrow MI=NF\) ( 2 cạnh tương ứng )

a,Xét \(\Delta AOB\)và \(\Delta COD\)có :
\(OC=OA\)(gt)
\(OD=OB\)(gt)
\(O_1=O_2\)(đối đỉnh)
\(=>\Delta AOB=\Delta COD\left(c-g-c\right)\)
b,Ta có :\(DCO=BAO\)(cm câu a)
Do 2 góc này ở vị trí so le trong và bằng nhau
\(=>AB//CD\)
Xét \(\Delta DAO\)và \(\Delta BCO\)có :
\(OC=OA\)(gt)
\(OB=OD\)(gt)
\(COB=AOD\)(đối đỉnh)
\(=>\Delta DAO=\Delta BCO\left(c-g-c\right)\)
\(=>ODA=OBC\)(2 góc tương ứng)
Do 2 góc này ở vị trí so le trong và bằng nhau
\(=>DA//BC\)
Gọi giao điểm của CE và DO là H
giao điểm của AO và BE là G
Lại có \(DCO=BAO=>\frac{DCO}{2}=\frac{BAO}{2}=>FAG=HCO\)
\(FGA=CGE\)( đối đỉnh)
Xét \(\Delta AGF\)và \(\Delta CGE\):
\(AFG+FGA+FAG=GEC+CGE+ECG=180^0\)
Do \(FAG+FGA=CGE+ECG\)
\(=>CEG=AFG\)
Vì 2 góc này ở vị trí so le trong và bằng nhau
\(=>CE//AF\)
c,Ta có \(CEB=AFG\)(cm câu b)
Mà \(AFG=\frac{CAB+DBA}{2}=\frac{CAB+CDB}{2}\)(CDB = DBA Ta cm ở câu a)
\(=>CEB=\frac{CAB+CDB}{2}\left(đpcm\right)\)
a, xét ΔAOB và ΔCOD có : OA = OC (Gt)
OB = OD (gt)
^AOB = ^COD (đối đỉnh)
=> ΔAOB = ΔCAOD (c-g-c)
b, ΔAOB = ΔCAOD (Câu a)
=> ^CDO = ^OBA (định nghĩa) mà 2 góc này so le trong
=> DC // AB (Định lí)
xét ΔODA và ΔOBC có : OA = OC (gt)
OB = OD (gt)
^DOA = ^BOC (đối đỉnh)
=> ΔODA = ΔOBC (c-g-c)
=> ^ADO = ^OBC (đn) mà 2 góc này so le trong
=> AD // BC (định lí)
ΔAOB = ΔCOD (câu a)
=> ^DCO = ^OAB (định nghĩa)
CE là phân giác của ^DCO (gt) => ^ECO = ^DCO : 2 (tính chất)
AF là phân giác của ^OAB (gt) => ^OAF = ^OAB : 2 (tính chất)
=> ^ECO = ^OAF mà 2 góc này so le trong
=> CE // AF (định lí)
c, mjnh không biết làm
giúp mình nhanh với ạ