Giả sử phương trình ax^2+bx+c=0 có hai nghiệm phân biệt là x1 và x2 khác 0. Hãy lập phương trình có nghiệm là :
a/ x12 và x22
b/ x1+x2 và x1x2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 3 2017
Đáp án: D
Theo định lý Vi-ét ta có
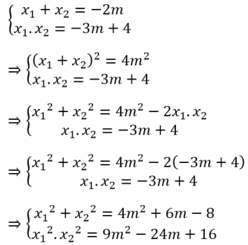
Khi đó, 
là nghiệm của phương trình
25 tháng 1 2023
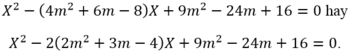
a: a=1; b=2m; c=-1
Vì a*c<0 nên (2) luôn có hai nghiệm phân biệt
b: \(x_1^2+x_2^2-x_1x_2=7\)
=>\(\left(x_1+x_2\right)^2-3x_1x_2=7\)
=>\(\left(-2m\right)^2-3\cdot\left(-1\right)=7\)
=>4m^2=7-3=4
=>m^2=1
=>m=1 hoặc m=-1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2022
\(\Delta'=1-\left(m-3\right)=4-m>0\Rightarrow m< 4\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
Do \(x_1+x_2=2\Rightarrow x_2=2-x_1\)
Ta có:
\(x_1^2+x_1x_2=2x_2-12\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)=2\left(2-x_1\right)-12\)
\(\Leftrightarrow2x_1=4-2x_1-12\)
\(\Leftrightarrow4x_1=-8\Rightarrow x_1=-2\Rightarrow x_2=4\)
Thế vào \(x_1x_2=m-3\Rightarrow m-3=-8\)
\(\Rightarrow m=-5\)
23 tháng 2 2022
a, \(\Delta'=\left(-m\right)^2-1\left(-1\right)=m^2+1>0\)
Vậy phương trình đã cho luôn có hai nghiệm phân biệt x1 và x2
b, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-1\end{matrix}\right.\)
\(x^2_1+x^2_2-x_1x_2=7\\ \Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=7\\ \Leftrightarrow\left(2m\right)^2-3\left(-1\right)=7\\ \Leftrightarrow4m^2+3=7\\ \Leftrightarrow4m^2=4\\ \Leftrightarrow m^2=1\\ \Leftrightarrow m=\pm1\)
CM
24 tháng 12 2017
Giả sử x 1 , x 2 la hai nghiệm của phương trình x 2 + px + q = 0
Theo hệ thức Vi-ét ta có: x 1 + x 2 = - p/1 = - p; x 1 x 2 = q/1 = q
Phương trình có hai nghiệm là x 1 + x 2 và x 1 x 2 tức là phương trình có hai nghiệm là –p và q.
Hai số -p và q là nghiệm của phương trình.
(x + p)(x - q) = 0 ⇔ x 2 - qx + px - pq = 0 ⇔ x 2 + (p - q)x - pq = 0
Phương trình cần tìm: x 2 + (p - q)x - pq = 0
12 tháng 2 2019
viết lại câu hỏi khác đi, đề không rõ ràng X với x rồi . lung tung, dung công cụ soạn thảo đi nha bạn
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
\(\Delta=1-4\left(m+1\right)>0\Rightarrow m< -\dfrac{3}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1^2+x_1x_2+3x_2=7\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)+3x_2=7\)
\(\Leftrightarrow x_1+3x_2=7\)
Kết hợp Viet ta được: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1+3x_2=7\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-2\\x_2=3\end{matrix}\right.\)
Thế vào \(x_1x_2=m+1\)
\(\Rightarrow m+1=-6\Rightarrow m=-7\)
