Cho 2001 điểm trên một mặt phẳng sao cho cứ một bộ ba điểm bất kì luôn có hai điểm có khoảng cách bé hơn 1.
Chứng minh rằng có ít nhất 1001 điểm nằm trong một đường tròn có bán kính bằng 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

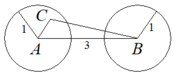
Nếu khoảng cách giữa hai điểm bất kì đều bé hơn 1 thì ta chỉ cần chọn 1 điểm \(A\) bất kì trong số 2001 điểm đã cho, rồi vẽ đường tròn \(\left(A,1\right)\), đường tròn này sẽ chứa cả 2000 điểm còn lại, do đó ta có đpcm.
Gỉa sử rằng có hai điểm \(A,B\) trong số 2001 điểm đã cho mà có khoảng cách lớn hơn \(1\). Vẽ các đường tròn tâm là \(A,B\) và bán kính cùng là \(1\). Ta còn lại 1999 điểm. Mỗi điểm \(C\) bất kì trong số 1999 điểm ấy, theo giả thiết \(AB,AC,BC\) phải có một đoạn có độ dài bé hơn \(1\). Vì \(AB>1\) nên \(AC

Gọi C là điểm bất kì trong 97 điểm còn lại
Ba điểm A,B,C lập thành một nhóm.
Theo giả thiết một nhóm bao giờ cũng có thể chọn ra hai điểm có khoảng cách nhỏ hơn 1cm

Theo nguyên lí Điriclê thì phải có một đường tròn chứa ít nhất 49 điểm.
Thêm điểm A hoặc B nữa thì có một đường tròn chứa ít nhất 50 điểm.