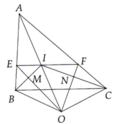
Cho tam giác ABC cân tại A , các phân giác BE , CF.
a) Chứng minh BFEC là hình thang cân
b) Chứng minh BF = FE = EC
c) Gọi giao điểm của BE và CF là O , trung điểm của EF là I , trung điểm của BC là J . Chứng minh 4 điểm A , I , O , J thẳng hàng
( KHI GIẢI KHÔNG CẦN VẼ HÌNH NHA ! )