cho hình vuông ABCD các điểm M,N lần lượt nằm trên AB và AD sao cho AM=AN Gọi H là hình chiếu của A trên DM. CMR: HN vuông góc với HC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có tam giác BHCBHC ∼AFH∼AFH
Vì AFBC=AEAB=AHBHAFBC=AEAB=AHBH
và gHBC=FAHgHBC=FAH (c−g−c)(c−g−c)
⇒BHC=AHF⇒BHC=AHF mà AHF+BHF=90⇒BHF+BHC=90AHF+BHF=90⇒BHF+BHC=90=> FH VUÔNG GÓC HC
⇒⇒ đpcm.

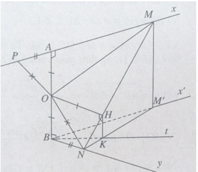
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

a: XétΔMAD vuông tại A và ΔNBA vuông tại B có
MA=NB
AD=BA
Do đó: ΔMAD=ΔNBA
=>DM=AN và \(\widehat{AMD}=\widehat{BNA}\)
=>\(\widehat{AMD}+\widehat{MAN}=90^0\)
=>DM vuông góc AN
b: AM+MB=AB
BN+NC=BC
mà AM=BN và AB=BC
nên MB=NC
Xét ΔMBC vuông tại B và ΔNCD vuông tại C có
MB=NC
BC=CD
Do đó: ΔMBC=ΔNCD
=>\(\widehat{BMC}=\widehat{CND}\)
=>\(\widehat{CND}+\widehat{NCM}=90^0\)
=>DN vuông góc MC
Xét ΔDMN có
CM,NA là đường cao
CM cắt NA tại X
Do đó: X là trực tâm
=>DX vuông góc MN

Do I là trực tâm của tam giác KAB nên K, I, H thẳng hàng.
Tứ giác AMIH nội tiếp nên \(\widehat{MHI}=\widehat{MAI}\).
Tương tự, \(\widehat{NHI}=\widehat{NBI}\).
Lại có \(\widehat{MAI}=\widehat{NBI}=90^o-\widehat{AKB}\) nên \(\widehat{MHI}=\widehat{NHI}\).
Vậy HK là phân giác của góc MHN.



đúng câu tớ đang làm