Nếu tử của một phân số tối giản bé hơn 1 được nâng lên lập phương còn mẫu số đc tăng lên 3 đơn vị thì phân số đã cho tăng lên gấp 3 lần . Tìm phân số đã cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 4 2020
Gọi phân số cần tìm là \(\frac{a}{b}\)với a<b và ƯCLN (a;b)=1
Theo bài ra ta có phương trình \(\frac{a^3}{b+3}=\frac{3a}{b}\Leftrightarrow a^3=3a+\frac{9a}{b}\)
Vì \(\frac{a}{b}< 1\Rightarrow a^3< 3a+9\)
- Nếu a=1 \(\Rightarrow b= -4\frac{2}{9}\)(loại)
- Nếu a=2 => b=9 ta có phân số thỏa mãn \(\frac{a}{b}=\frac{2}{9}\)
- Nếu \(a\ge3\)thì \(a^3\ge3a+9\)(vô lý)
Đáp số \(\frac{a}{b}=\frac{2}{9}\)
DA
1 tháng 3 2015
gọi tử số của phân số cần tìm là x (x>0)
theo bài phân số ban đầu là x / (x+13)
do đó (x +3) / (x+13 - 5 ) = 3 / 4
<=> 4(x+3) = 3(x+8)
<=>4x + 12 = 3x +24
<=>x = 12
<=>phân số cần tìm là 12 / (12+13) = 12 / 25
vậy phân số cần tìm là 12 / 25
19 tháng 3 2020
Gọi tử số là x
Mẫu số sẽ là : x + 11 ( x khác -11)
Ta có phân số đó là: \(\frac{x}{x+11}\)
Bớt tử số 7 đơn vị và tăng mẫu số lên 4 đơn vị ta có: \(\frac{x-7}{x+15}\)( x khác -15)
Theo bài ra ta có phương trình: \(\frac{x-7}{x+15}=\frac{x+11}{x}\)( x khác 0; -11; -15)
<=> \(x\left(x-7\right)=\left(x+11\right)\left(x+15\right)\)
<=> \(x^2-7x=x^2+26x+165\)
<=> \(x=-5\)
Vậy phân số đó là: \(\frac{-5}{6}\)
BH
14 tháng 2 2019
gọi a là tử số thì a+13 là mẫu số
nếu tăng tử thêm 3 ,giảm mẫu đi 5 thì được phân số mới là 5/4 nên
\(\frac{a+3}{a+13-5}=\frac{5}{4}\Leftrightarrow\frac{a+3}{a+8}=\frac{5}{4}\)
nên 4(a+3)=5(a+8)
4a+12=5a+40
a=-28
nên tử số là -28
mẫu số là -28+13=-15
nên phân số cần tìm là -28/-15=28/15
hihiihi
NT
30 tháng 7 2015
Gọi tử số của phấn số cần tìm là x thì mẫu số của phân số cần tìm là x+11. Phân số cần tìm là \(\frac{x}{x+11}\)( x là số nguyên khác -11)
Khi bớt tử số đi 7 đơn vị và tăng mẫu lên 4 đơn vị ta được phân số
\(\frac{x-7}{x+15}\)(x khác -15)
theo bài ra ta có phương trình \(\frac{x}{x+11}=\frac{x+15}{x-7}\)
giải phương trình và tìm được x=-5 ( thỏa mãn)
từ đó tìm được phấn số \(-\frac{5}{6}\)
CM
27 tháng 10 2019
Gọi tử số của phân số cần tìm là x (x ϵ Z)
Mẫu số của phân số đó là x + 11
Ta được phân số: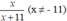 
Khi giảm tử số đi 7 đơn vị ta được x – 7, tăng mẫu lên 4 đơn vị thì mẫu mới là x + 15
được phân số mới là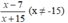 
phân số mới là nghịch đảo của phân số ban đầu nên ta có:
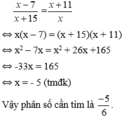
\(\frac{12}{25}\)en hok lop 7\(y=\frac{1}{x^2+\sqrt{x}}\)