để chuẩn bị thi một sinh viên được cho hai tập câu hỏi để ôn tập mỗi tập gồm 10 câu. Giả sử trước khi thi anh ta học thuộc 9 câu của tập 1 và 8 câu ở tập 2. Để thi gồm 3 câu thiết kế như sau: Chọn ngẫu nhiên một tập câu hỏi rồi ngẫu nhiên chọn 2 câu . Câu thứ 3 chọn ngẫu nhiên từ tập còn lại. Tính xác suất để sinh viên trả lời đúng 2 câu.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Số cách chọn 2 trong 20 câu lí thuyết là: \(C_{20}^2\)
Số cách chọn ra 3 trong 40 câu bài tập là: \(C_{40}^3\)
=> Số cách lập đề thi gồm 5 câu hỏi như trên là: \(C_{20}^2.C_{40}^3 = 1877200\)
CM
4 tháng 8 2019
Đáp án A
Ta xét 2 trường hợp:
TH1: Đề thi có 9 câu hỏi nằm trong 25 câu mà học sinh nắm được ⇒ P 1 = C 25 9 . C 5 1 C 30 10
TH2: Đề thi có 10 câu hỏi nằm trong 25 câu mà học sinh nắm được ⇒ P 2 = C 25 10 C 30 10
Vậy xác suất cần tính là P = P 1 + P 2 = 0 , 449
CM
7 tháng 2 2019
Đáp án A
Ta xét 2 trường hợp
TH1:
Đề thi có 9 câu hỏi nằm trong 25 câu mà học sinh nắm được
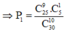
TH2:
Đề thi có 10 câu hỏi nằm trong 25 câu mà học sinh nắm được
Vậy xác suất cần tính là
CM
19 tháng 10 2017
Chọn đáp án C.
* TH1: Đề thi gồm 1 câu lý thuyết và 2 câu bài tập
Số cách tạo đề thi: C 4 1 . C 6 2 cách
* TH2: Đề thi gồm 2 câu lý thuyết và 1 câu bài tập
Số cách tạo đề thi: C 4 2 . C 6 1 cách
* KL: Số cách tạo đề thi: C 4 1 . C 6 2 + C 4 2 . C 6 1 = 96 cách
CM
15 tháng 4 2019
Phương pháp
Sử dụng quy tắc cộng để làm bài toán.
Cách giải
Để chọn được 3 câu hỏi trong đó có ít nhất 1 câu lý thuyết và 1 câu bài tập ta chia thành 2 TH:
TH1: Chọn 1 câu lý thuyết và 2 câu bài tập có: C 4 1 . C 6 2 cách chọn.
TH2: Chọn 2 câu lý thuyết và 1 câu bài tập có: C 4 2 . C 6 1 cách chọn.
Như vậy có: C 4 1 . C 6 2 + C 4 2 . C 6 1 = 96 cách chọn.
Chọn C.
HT
7 tháng 2 2021
Ít nhất 1 câu hình học, nhiều nhất là 3 câu hình học, bởi giới hạn chỉ được bốc 3 câu hỏi
Khong gian mau: \(n\left(\Omega\right)=C^3_{15}\)
TH1: Bốc 1 câu hình học và 2 câu đại số
\(C^1_5.C^2_{10}\)
TH2: Bốc 2 câu hình học và 1 câu đại số
\(C^2_5.C^1_{10}\)
TH3: Bốc 3 câu hình học
\(C^3_5\)
\(\Rightarrow C^1_5.C^2_{10}+C^2_5.C^1_{10}+C^3_5=..\)
\(p\left(A\right)=\dfrac{C^1_5.C^2_{10}+C^2_5.C^1_{10}+C^3_5}{C^3_{15}}=...\)
7 tháng 2 2021
Ω: "Chọn 3 câu hỏi từ 15 câu."
⇒ n(Ω) = \(C^3_{15}=455\)
A: "Chọn được ít nhất 1 câu hỏi Hình học."
⇒ \(\overline{A}\): "Không chọn được câu Hình học nào."
\(\Rightarrow n\left(\overline{A}\right)=C^3_{10}=120\)
\(\Rightarrow P\left(\overline{A}\right)=\dfrac{120}{455}=\dfrac{24}{91}\)
\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=\dfrac{67}{91}\)
Bạn tham khảo nhé!